题目内容
下列命题是真命题的为( )
| A、?x∈R,2x-1>0 | ||||||||||
B、若sinx=cosy,则x+y=
| ||||||||||
C、若
| ||||||||||
| D、若x<y,则x2<y2 |
分析:由指数函数的性质,可判断选项A正确;通过举反例,可判断选项B、C、D均错误.
解答:解:A:因为?x∈R,2x>0恒成立,所以2x-1=
>0恒成立,所以选项A正确;
B:若sinx=cosy,如x=0,y=
,则不满足x+y=
,所以选项B错误;
C:若
∥
,如
=(1,2),
=(2,4),则
+
=(3,6)≠
,所以选项C错误;
D:若x<y,如x=-2,y=1,则x2>y2,不满足x2<y2,所以选项D错误.
故选A.
| 2x |
| 2 |
B:若sinx=cosy,如x=0,y=
| 3π |
| 2 |
| π |
| 2 |
C:若
| a |
| b |
| a |
| b |
| a |
| b |
| 0 |
D:若x<y,如x=-2,y=1,则x2>y2,不满足x2<y2,所以选项D错误.
故选A.
点评:证明全称命题的基本策略:证明全称命题成立,需严格的逻辑推理;证明全称命题不成立,只需举一反例即可.

练习册系列答案
相关题目
下列命题是真命题的为( )
A、若
| ||||
| B、若x2=1,则x=1 | ||||
C、若x=y,则
| ||||
| D、若x<y,则x2<y2 |
下列命题是真命题的为( )
| A、“若a,b,c是等比数列,则b2=ac”的逆命题 | ||||||||||||
| B、“平行于同一条直线的两条直线平行,若a∥c,b∥c,则a∥b”这是一个“三段论” | ||||||||||||
| C、“?x∈R,x2+1≥1”的否定 | ||||||||||||
D、“向量
|
 ,对
,对 都有
都有 ,则
,则 为偶函数
为偶函数 ,若对
,若对 ,都有
,都有 ,则函数
,则函数 中心对称
中心对称 与
与 是奇函数
是奇函数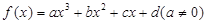 的图形一定是对称中心在图像上的中心对称图形。
的图形一定是对称中心在图像上的中心对称图形。 有两不同极值点
有两不同极值点 ,若
,若 ,且
,且 ,则关于的方程
,则关于的方程 的不同实根个数必有三个.
的不同实根个数必有三个.