题目内容
已知函数f(x)＝2cos 2x＋sin2x－4cos x.
(1)求f(
)的值；
(2)求f(x)的最大值和最小值．
解：(1)f()＝2cos
＋sin2－4cos
＝－1＋
－2＝－
.
(2)f(x)＝2(2cos2x－1)＋(1－cos2x)－4cos x
＝3cos2x－4cosx－1＝3
2－
，x∈R.
因为cosx∈[－1
,1]，
所以，当cosx＝－1时，f(x)取得最大值6；
当cos x＝
时，f(x)取得最小值－.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
，π)，且sin
＋cos
.
，β∈(
＝－
，则sin2x的值为( )
.
B．－
)上是增函数，则实数φ可能是( )
B．0
(x∈R)，有下列命题：
；
对称；
对称．
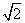的等比数列，则其最大角的余弦值为________．