题目内容
（改编）定义在R上的函数f(x)满足f(x)=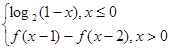 
，则f（2012）的值为( )
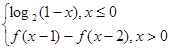，则f（2012）的值为( )| A．0 | B．1 | C．-1 | D．2 |
C
分析：利用函数的表达式求出f（-1）=1，f（0）=0，f（1）=f（2）=-1，f（3）=0，f（4）=f（5）=1，f（6）=0，找出规律，然后求出f（2012）的值．
解：因为定义在R上的函数f（x）满足f(x)=
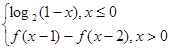，所以f（-1）=1，f（0）=0，f（1）=f（2）=-1，f（3）=0，f（4）=f（5）=1，f（6）=0，
当k∈Z时，f（1+6k）=f（2+6k）=-1，f（3+6k）=0，f（4+6k）=f（5+6k）=1，f（6k）=0，
f（2012）=f（6×335+2）=-1．
故答案为：-1．
练习册系列答案
相关题目
与函数
的图象关于（ ）
轴对称
对称
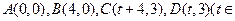R)。记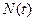
为平行四边形ABCD内部（不含边界）的整点的个数，其中整点是指横、纵坐标都是整数的点，则
；
，
为实数，（
）．
，求函数
的极值；
,且函数
，若函数
有3个零点，则实数
的
）
,若
,则实数
=____
则
.