题目内容
函数
的一条对称轴方程是
- A.
- B.
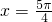
- C.
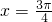
- D.
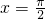
D
分析：利用诱导公式化简函数解析式，令2x=k π，k∈z，解出x=
，k∈z即为所求．
解答：函数=-cos2x，
令2x=kπ，k∈z，可得x=，k∈z，
故选D．
点评：本题考查诱导公式，余弦函数的对称性，过图象的顶点垂直于x轴的直线都是余弦函数的对称轴．
分析：利用诱导公式化简函数解析式，令2x=k π，k∈z，解出x=
，k∈z即为所求．解答：函数
=-cos2x，令2x=kπ，k∈z，可得x=
，k∈z，故选D．
点评：本题考查诱导公式，余弦函数的对称性，过图象的顶点垂直于x轴的直线都是余弦函数的对称轴．
练习册系列答案
相关题目
已知函数y=2sin(2x+φ)(|φ|＜
)的图象经过点（0，1），则该函数的一条对称轴方程为（ ）
| π |
| 2 |
A、x=-
| ||
B、x=-
| ||
C、x=
| ||
D、x=
|
把函数y=sin（ωx+φ）（其中φ为锐角）的图象向右平移
个单位或向左平移
个单位都可使对应的新函数成为奇函数，则原函数的一条对称轴方程是（ ）
| π |
| 8 |
| 3π |
| 8 |
A、x=
| ||
B、
| ||
C、x=-
| ||
D、
|
是周期为
的偶函数；
是第一象限的角，且
，则
；
是函数
的一条对称轴方程；
内方程
有3个解.
,使
是偶函数 
是函数
的一条对称轴方程
是第一象限的角，且
，则