Question

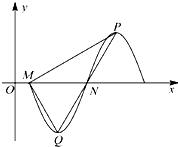
在函数y=acos（ax+θ）（a，θ∈R，aθ≠0）的图象上，同一周期内的最高点与最低点之间距离的最小值为

 

．

Answer 1

分析：求出函数的最大值，函数的周期，通过直角三角形，利用基本不等式即可求出同一周期内的最高点与最低点之间距离的最小值．

解答：解：函数y=acos（ax+θ）的最大值为：|a|，周期为 T=

2π

|a|

，
同一周期内的最高点与最低点之间距离为：

(2|a|)2+( T 2 )2

=

(2a)2+( π a )2

≥

4π

=2

π

故答案为：2

π

点评：本题是基础题，考查三角函数图象的理解，三角函数的最值、周期的应用，基本不等式的应用，考查计算能力．