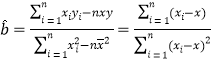题目内容
【题目】(本小题满分14分)
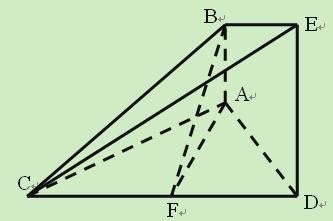
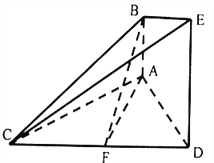
如图的几何体中, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,△
,△![]() 为等边三角形
为等边三角形![]() ,
, ![]() 为
为![]() 的中点.
的中点.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() 。
。
【答案】(1)证明:取![]() 的中点
的中点![]() ,连结
,连结![]() .
.
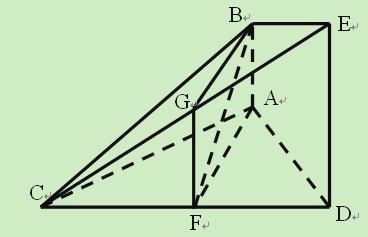
∵![]() 为
为![]() 的中点,∴
的中点,∴![]() 且
且![]() .
.
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() ,∴
,∴![]() .
.
又![]() ,∴
,∴![]() . …………3分
. …………3分
∴四边形![]() 为平行四边形,则
为平行四边形,则![]() .……………5分
.……………5分
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .…………7分
.…………7分
(2)证明:∵![]() 为等边三角形,
为等边三角形, ![]() 为
为![]() 的中点,∴
的中点,∴![]() …………9分
…………9分
∵![]() 平面
平面![]() ,
, ![]() ,∴
,∴![]() .……………10分
.……………10分
又![]() ,∴
,∴![]() 平面
平面![]() .……………………………12分
.……………………………12分
∵![]() ,∴
,∴![]() 平面
平面![]() .…………………………………13分
.…………………………………13分
∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .………………14分
.………………14分
【解析】试题分析:(1)通过取![]() 的中点
的中点![]() ,利用三角形的中位线定理和平行四边形的性质及线面平行的判定定理即可证明;(2)连接
,利用三角形的中位线定理和平行四边形的性质及线面平行的判定定理即可证明;(2)连接![]() ,设
,设![]() 到平面
到平面![]() 的距离为
的距离为![]() ,利用等体积法
,利用等体积法![]() 可求得结果.
可求得结果.
试题解析:(1)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() .
.
∵![]() 为
为![]() 的中点,∴
的中点,∴![]() 且
且![]() .
.
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() ,∴
,∴![]() ,
,
又![]() ,∴
,∴![]() .
.
∴四边形![]() 为平行四边形,则
为平行四边形,则![]() .
.
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)连接![]() ,设
,设![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
在![]() 中,
中, ![]() ,
, ![]() ,
,
∴![]() ,
,
又![]() ,
, ![]() ,
,
∴由![]() ,即
,即![]() (
(![]() 为正
为正![]() 的高),
的高),
∴![]()
即点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.

【题目】某民调机构为了了解民众是否支持英国脱离欧盟,随机抽调了100名民众,他们的年龄的频数及支持英国脱离欧盟的人数分布如下表:
年龄段 | 18-24岁 | 25-49岁 | 50-64岁 | 65岁及以上 |
频数 | 35 | 20 | 25 | 20 |
支持脱欧的人数 | 10 | 10 | 15 | 15 |
(Ⅰ)由以上统计数据填下面列联表,并判断是否有99%的把握认为以50岁胃分界点对是否支持脱离欧盟的态度有差异;
年龄低于50岁的人数 | 年龄不低于50岁的人数 | 合计 | |
支持“脱欧”人数 | |||
不支持“脱欧”人数 | |||
合计 |
附:![]()

(Ⅱ)若采用分层抽样的方式从18-64岁且支持英国脱离欧盟的民众中选出7人,再从这7人中随机选出2人,求这2人至少有1人年龄在18-24岁的概率.