题目内容
设正数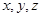 ,
,
(1)满足 ,求证:
,求证: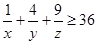 ;
;
(2)若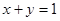 ,求
,求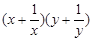 的最小值。
的最小值。
(1)不等式的证明,可以运用均值不等式来得到证明。
(2)根据均值不等式的一正二定三相等来求解最值。
解析试题分析:⑴证明:(利用柯西不等式)
⑵根据题意,由于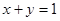 ,那么
,那么 ,在可以根据均值不等式同时取得等号得到其最小值为
,在可以根据均值不等式同时取得等号得到其最小值为
考点:均值不等式
点评:主要是考查了不等式的证明以及最值的求解,属于中档题。

练习册系列答案
相关题目
题目内容
设正数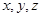 ,
,
(1)满足 ,求证:
,求证: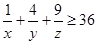 ;
;
(2)若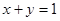 ,求
,求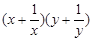 的最小值。
的最小值。
(1)不等式的证明,可以运用均值不等式来得到证明。
(2)根据均值不等式的一正二定三相等来求解最值。
解析试题分析:⑴证明:(利用柯西不等式)
⑵根据题意,由于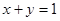 ,那么
,那么 ,在可以根据均值不等式同时取得等号得到其最小值为
,在可以根据均值不等式同时取得等号得到其最小值为
考点:均值不等式
点评:主要是考查了不等式的证明以及最值的求解,属于中档题。
