题目内容
若不等式组
表示的区域面积为S,则
(1)当S=2时,k=______;
(2)当k>1时,
的最小值为______.
|
(1)当S=2时,k=______;
(2)当k>1时,
| kS |
| k-1 |
(1)∵直线l:y=-kx+4k=-k(x-4)
∴直线l经过点A(4,0),令x=0,得y=4k,直线l交y轴于点B(0,4k)
因此,不等式组
表示的区域是图中△AOB,
其面积为S=
×|OA|×|OB|=8k=2,解之得k=
;
(2)由(1),得S=8k,可得
=
=
,其中k>1
=8(k-1)+
+16,
∵8(k-1)+
≥2
=16
∴当且仅当8(k-1)=
时,即k=2时,8(k-1)+
的最小值为16,
由此可得
≥16+16=32,即k>1时,
的最小值为32
故答案为:
,32

∴直线l经过点A(4,0),令x=0,得y=4k,直线l交y轴于点B(0,4k)
因此,不等式组
|
其面积为S=
| 1 |
| 2 |
| 1 |
| 4 |
(2)由(1),得S=8k,可得
| kS |
| k-1 |
| k(8k) |
| k-1 |
| 8k2 |
| k-1 |
| 8k2 |
| k-1 |
| 8 |
| k-1 |
∵8(k-1)+
| 8 |
| k-1 |
8(k-1)×
|
∴当且仅当8(k-1)=
| 8 |
| k-1 |
| 8 |
| k-1 |
由此可得
| 8k2 |
| k-1 |
| kS |
| k-1 |
故答案为:
| 1 |
| 4 |

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
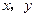 满足
满足 则
则 的最大值是 .
的最大值是 .