题目内容
若点P(x,y)在曲线(x+2)2+y2=1上,则| y | x |
分析:利用z=
的几何意义求最值,只需求出曲线(x+2)2+y2=1上的点到原点的连线的斜率的最值,从而得到z最值即可.
| y |
| x |
解答: 解:画图如下,
解:画图如下,
设z=
将z=
的几何意义看作是经过点(0,0)和(x,y)的
直线斜率,可得当过A(1,5)时,z的最小值是-
.
由对称性知,z的最大值是
.
故填:[-
,
].
 解:画图如下,
解:画图如下,设z=
| y |
| x |
将z=
| y |
| x |
直线斜率,可得当过A(1,5)时,z的最小值是-
| ||
| 3 |
由对称性知,z的最大值是
| ||
| 3 |
故填:[-
| ||
| 3 |
| ||
| 3 |
点评:本小题是考查线性规划问题,本题主要考查了简单的线性规划,以及利用几何意义求最值,属于基础题.

练习册系列答案
相关题目
 (2012•湖南)函数f(x)=sin (ωx+φ)的导函数y=f′(x)的部分图象如图所示,其中,P为图象与y轴的交点,A,C为图象与x轴的两个交点,B为图象的最低点.
(2012•湖南)函数f(x)=sin (ωx+φ)的导函数y=f′(x)的部分图象如图所示,其中,P为图象与y轴的交点,A,C为图象与x轴的两个交点,B为图象的最低点.
 如图,成都市准备在南湖的一侧修建一条直路EF,另一侧修建一条观光大道,大道的前一部分为曲线段FBC,该曲线段是函数
如图,成都市准备在南湖的一侧修建一条直路EF,另一侧修建一条观光大道,大道的前一部分为曲线段FBC,该曲线段是函数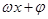 )的导函数
)的导函数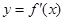 的部分图像如图所示,其中,P为图像与y轴的交点,A,C为图像与x轴的两个交点,B为图像的最低点.
的部分图像如图所示,其中,P为图像与y轴的交点,A,C为图像与x轴的两个交点,B为图像的最低点.
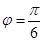 ,点P的坐标为(0,
,点P的坐标为(0,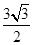 ),则
),则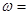 ;
;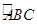 与x轴所围成的区域内随机取一点,则该点在△ABC内的概率为 .
与x轴所围成的区域内随机取一点,则该点在△ABC内的概率为 .