题目内容
已知双曲线 与椭圆
与椭圆 有共同的焦点,点
有共同的焦点,点 在双曲线C上.
在双曲线C上.(1)求双曲线C的方程;
(2)以P(1,2)为中点作双曲线C的一条弦AB,求弦AB所在直线的方程.
【答案】分析:(1)由椭圆方程可求其焦点坐标,从而可得双曲线C的焦点坐标,利用点 在双曲线C上,根据双曲线定义||AF1|-|AF2||=2a,即可求出所求双曲线C的方程;
在双曲线C上,根据双曲线定义||AF1|-|AF2||=2a,即可求出所求双曲线C的方程;
(2)设A(x1,y1),B(x2,y2),代入A、B在双曲线方程得 ,两方程相减,借助于P(1,2)为中点,可求弦AB所在直线的斜率,进而可求其方程.
,两方程相减,借助于P(1,2)为中点,可求弦AB所在直线的斜率,进而可求其方程.
解答:解:(1)由已知双曲线C的焦点为F1(-2,0),F2(2,0)
由双曲线定义||AF1|-|AF2||=2a,
∴
∴ ,
,
∴b2=2
∴所求双曲线为 …(6分)
…(6分)
(2)设A(x1,y1),B(x2,y2),因为A、B在双曲线上
∴ ,两方程相减得:得(x1-x2)(x1+x2)-(y1-y2)(y1+y2)=0
,两方程相减得:得(x1-x2)(x1+x2)-(y1-y2)(y1+y2)=0
∴ ,
,
∴
∴弦AB的方程为 即x-2y+3=0
即x-2y+3=0
经检验x-2y+3=0为所求直线方程.…(12分)
点评:本题以椭圆为载体,考查双曲线的标准方程,考查弦中点问题,考查点差法的运用,综合性强.
 在双曲线C上,根据双曲线定义||AF1|-|AF2||=2a,即可求出所求双曲线C的方程;
在双曲线C上,根据双曲线定义||AF1|-|AF2||=2a,即可求出所求双曲线C的方程;(2)设A(x1,y1),B(x2,y2),代入A、B在双曲线方程得
 ,两方程相减,借助于P(1,2)为中点,可求弦AB所在直线的斜率,进而可求其方程.
,两方程相减,借助于P(1,2)为中点,可求弦AB所在直线的斜率,进而可求其方程.解答:解:(1)由已知双曲线C的焦点为F1(-2,0),F2(2,0)
由双曲线定义||AF1|-|AF2||=2a,
∴

∴
 ,
,∴b2=2
∴所求双曲线为
 …(6分)
…(6分)(2)设A(x1,y1),B(x2,y2),因为A、B在双曲线上
∴
 ,两方程相减得:得(x1-x2)(x1+x2)-(y1-y2)(y1+y2)=0
,两方程相减得:得(x1-x2)(x1+x2)-(y1-y2)(y1+y2)=0∴
 ,
,∴

∴弦AB的方程为
 即x-2y+3=0
即x-2y+3=0经检验x-2y+3=0为所求直线方程.…(12分)
点评:本题以椭圆为载体,考查双曲线的标准方程,考查弦中点问题,考查点差法的运用,综合性强.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
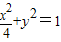 共焦点,它们的离心率之和为
共焦点,它们的离心率之和为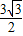 ;
;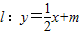 与椭圆有两个交点,求m的取值范围.
与椭圆有两个交点,求m的取值范围. ,且与椭圆
,且与椭圆 有共同的焦点.
有共同的焦点.