题目内容
已知双曲线与椭圆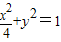 共焦点,它们的离心率之和为
共焦点,它们的离心率之和为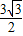 ;
;(1)求椭圆与双曲线的离心率e1、e2;
(2)求双曲线的标准方程与渐近线方程;
(3)已知直线
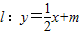 与椭圆有两个交点,求m的取值范围.
与椭圆有两个交点,求m的取值范围.
【答案】分析:(1)椭圆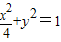 中,由a=2,c=
中,由a=2,c=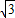 ,能求出椭圆离心率e1,由双曲线与椭圆离心率之和为
,能求出椭圆离心率e1,由双曲线与椭圆离心率之和为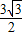 ,能求出双曲线的离心率e2.
,能求出双曲线的离心率e2.
(2)由椭圆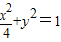 焦点为F1(-
焦点为F1(-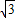 ,0),F2(
,0),F2(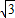 ,0),双曲线与椭圆
,0),双曲线与椭圆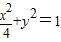 共焦点,知双曲线的焦点为F1(-
共焦点,知双曲线的焦点为F1(-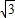 ,0),F2(
,0),F2(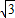 ,0),再由双曲线的离心率e2=
,0),再由双曲线的离心率e2=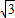 .能求出双曲线的标准方程和渐近线方程.
.能求出双曲线的标准方程和渐近线方程.
(3)由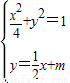 ,得2x2+4mx+4m2-4=0,直线
,得2x2+4mx+4m2-4=0,直线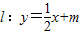 与椭圆有两个交点,知△=(4m)2-8(4m2-4)>0,由此能求出m的取值范围.
与椭圆有两个交点,知△=(4m)2-8(4m2-4)>0,由此能求出m的取值范围.
解答:解:(1)∵椭圆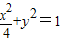 中,
中,
a=2,c=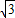
∴椭圆离心率e1=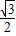 .
.
∵双曲线与椭圆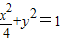 的离心率之和为
的离心率之和为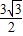 ,
,
∴双曲线的离心率e2=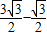 =
=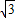 .
.
(2)∵椭圆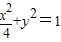 焦点为F1(-
焦点为F1(-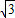 ,0),F2(
,0),F2(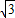 ,0),
,0),
双曲线与椭圆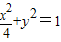 共焦点,
共焦点,
∴双曲线的焦点为F1(-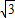 ,0),F2(
,0),F2(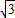 ,0),
,0),
∵双曲线的离心率e2=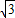 .
.
∴双曲线的标准方程为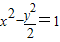 ,
,
∴双曲线的渐近线方程为y=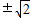 x.
x.
(3)由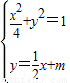 ,得2x2+4mx+4m2-4=0,
,得2x2+4mx+4m2-4=0,
∵直线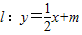 与椭圆有两个交点,
与椭圆有两个交点,
∴△=(4m)2-8(4m2-4)>0,
解得-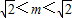 .
.
故m的取值范围是(-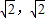 ).
).
点评:本题考查直线与圆锥曲线的位置关系的求法,解题时要认真审题,仔细解答,注意等价转化思想的合理运用.
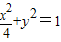 中,由a=2,c=
中,由a=2,c=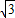 ,能求出椭圆离心率e1,由双曲线与椭圆离心率之和为
,能求出椭圆离心率e1,由双曲线与椭圆离心率之和为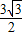 ,能求出双曲线的离心率e2.
,能求出双曲线的离心率e2.(2)由椭圆
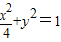 焦点为F1(-
焦点为F1(-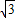 ,0),F2(
,0),F2(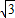 ,0),双曲线与椭圆
,0),双曲线与椭圆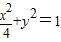 共焦点,知双曲线的焦点为F1(-
共焦点,知双曲线的焦点为F1(-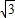 ,0),F2(
,0),F2(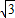 ,0),再由双曲线的离心率e2=
,0),再由双曲线的离心率e2=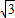 .能求出双曲线的标准方程和渐近线方程.
.能求出双曲线的标准方程和渐近线方程.(3)由
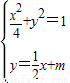 ,得2x2+4mx+4m2-4=0,直线
,得2x2+4mx+4m2-4=0,直线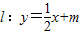 与椭圆有两个交点,知△=(4m)2-8(4m2-4)>0,由此能求出m的取值范围.
与椭圆有两个交点,知△=(4m)2-8(4m2-4)>0,由此能求出m的取值范围.解答:解:(1)∵椭圆
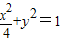 中,
中,a=2,c=
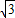
∴椭圆离心率e1=
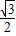 .
.∵双曲线与椭圆
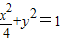 的离心率之和为
的离心率之和为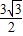 ,
,∴双曲线的离心率e2=
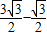 =
=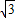 .
.(2)∵椭圆
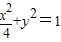 焦点为F1(-
焦点为F1(-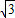 ,0),F2(
,0),F2(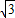 ,0),
,0),双曲线与椭圆
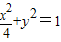 共焦点,
共焦点,∴双曲线的焦点为F1(-
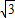 ,0),F2(
,0),F2(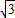 ,0),
,0),∵双曲线的离心率e2=
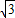 .
.∴双曲线的标准方程为
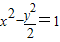 ,
,∴双曲线的渐近线方程为y=
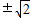 x.
x.(3)由
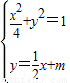 ,得2x2+4mx+4m2-4=0,
,得2x2+4mx+4m2-4=0,∵直线
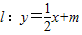 与椭圆有两个交点,
与椭圆有两个交点,∴△=(4m)2-8(4m2-4)>0,
解得-
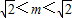 .
.故m的取值范围是(-
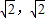 ).
).点评:本题考查直线与圆锥曲线的位置关系的求法,解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 共焦点,它们的离心率之和为
共焦点,它们的离心率之和为 ,则双曲线的方程应是
,则双曲线的方程应是
 共焦点,它们的离心率之和为
共焦点,它们的离心率之和为 ,则双曲线方程为_____
,则双曲线方程为_____ 共焦点,它们的离心率之和为
共焦点,它们的离心率之和为 ,求双曲线的标准方程。
,求双曲线的标准方程。 共焦点,且以
共焦点,且以 为渐近线,求双曲线的标准方程和离心率
为渐近线,求双曲线的标准方程和离心率