Question

已知函数。

    （I）当时，解不等式；

    （II）求的最大值。

Answer 1

解：（I）当时，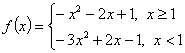

    原不等式等价于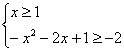，或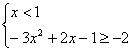

    故原不等式的解集为；

    （II）∵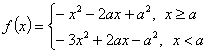

即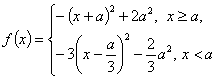

    ①当时，在上单减，最大值为，

在上先增后减，最大值为，

此时，在上最大值为；

②当时，在上先增后减，最大值为，

在上单增，最大值为，

此时，上最大值为

③当时，在上最大值为0。

综上，当时，最大值为；当时，最大值为。