题目内容
已知三个向量 =(cosθ1,sinθ1),
=(cosθ1,sinθ1), =(cosθ2,sinθ2),
=(cosθ2,sinθ2), =(cosθ3,sinθ3),满足
=(cosθ3,sinθ3),满足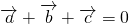 ,则
,则 与
与 的夹角为________.
的夹角为________.

分析:先利用向量的坐标运算得到两个三角方程,两式平方相加,根据向量夹角的范围为[0,π],即可得到结论.
解答:由题意,∵
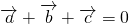 ,∴cosθ1+cosθ2=-cosθ3,sinθ1+sinθ2=-sinθ3,
,∴cosθ1+cosθ2=-cosθ3,sinθ1+sinθ2=-sinθ3,两式平方相加可得:2+2cos(θ1-θ2)=1
∴cos(θ1-θ2)=-

∵向量夹角的范围为[0,π]
∴θ1-θ2=

故答案为:

点评:本题以向量为载体,考查向量的坐标运算,考查向量的夹角,解题的关键是列出两个三角方程.

练习册系列答案
相关题目
