题目内容
12.函数f(x)=$\sqrt{2}$(sinωx+cosωx)(ω>0)对任意实数x都有f($\frac{π}{4}$+x)=f($\frac{π}{4}$-x),则f($\frac{π}{4}$)等于( )| A. | $\sqrt{2}$或0 | B. | -2或2 | C. | $\sqrt{2}$或-$\sqrt{2}$ | D. | -$\sqrt{2}$或0 |
分析 利用两角和的正弦公式化简函数的解析式为f(x)=2sin(ωx+$\frac{π}{4}$),根据f($\frac{π}{4}$+x)=f($\frac{π}{4}$-x),可得故函数的图象关于直线x=$\frac{π}{4}$对称,有ω=4k+1,k∈z,解得ω的值,代入x=$\frac{π}{4}$,化简即可求得结果.
解答 解:∵函数f(x)=$\sqrt{2}$(sinωx+cosωx)=2sin(ωx+$\frac{π}{4}$),
对任意实数x都有f($\frac{π}{4}$+x)=f($\frac{π}{4}$-x),
故函数的图象关于直线x=$\frac{π}{4}$对称,
故有ω•$\frac{π}{4}$+$\frac{π}{4}$=kπ+$\frac{π}{2}$,k∈z,
∴ω=4k+1,k∈z,
令k=0,可得:ω=1,则f($\frac{π}{4}$)=$\sqrt{2}$(sin$\frac{π}{4}$+cos$\frac{π}{4}$)=$\sqrt{2}$×($\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}$)=2.
令k=1,可得:ω=5,则f($\frac{π}{4}$)=$\sqrt{2}$(sin$\frac{5π}{4}$+cos$\frac{5π}{4}$)=$\sqrt{2}$×[-($\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}$)]=-2.
故选:B.
点评 本题主要考查两角和的正弦公式,正弦函数的对称性,属于中档题.

练习册系列答案
相关题目
2.若实数数列:1,a,81成等比数列,则圆锥曲线x2+$\frac{y^2}{a}$=1的离心率是( )
| A. | $\sqrt{10}$ 或$\frac{{2\sqrt{2}}}{3}$ | B. | $\sqrt{3}$或$\frac{{\sqrt{6}}}{3}$ | C. | $\frac{{2\sqrt{2}}}{3}$ | D. | $\frac{1}{3}$或10 |
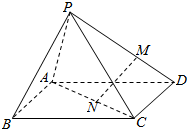 如图,设P为长方形ABCD所在平面外一点,M在PD上,N在AC上,若$\frac{DM}{MP}$=$\frac{CN}{NA}$,用向量法证明:直线MN∥平面PAB.
如图,设P为长方形ABCD所在平面外一点,M在PD上,N在AC上,若$\frac{DM}{MP}$=$\frac{CN}{NA}$,用向量法证明:直线MN∥平面PAB.