题目内容
已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的2个红球和4个黑球.现从甲、乙两个盒内各任取2个球.
(1)求取出的4个球均为黑球的概率;
(2)求取出的4个球中恰有1个红球的概率;
(3)设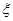 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求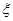 的分布列.
的分布列.
(1) ;(2)
;(2) ;(3)
;(3)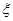 的分布列为
的分布列为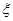
1 2 3 4 




解析试题分析:(1)设“取出的4个球均为黑球”为事件 ,
, ;
;
(2)设“取出的4个球恰有1个红球”为事件 ,
, ;
;
(3)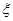 所有可能的值为0,1,2,3,4,
所有可能的值为0,1,2,3,4, , 8分
, 8分 , 10分
, 10分 , 12分
, 12分 14分
14分
所以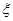 的分布列为
的分布列为
15分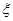
1 2 3 4 




考点:本题考查了概率与统计
点评:在求概率时,应注意立事件概率公式的应用,还有区分是属于什么事件.求分布列时要掌握分布列的概念及性质

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
我区高三期末统一测试中某校的数学成绩分组统计如下表:
| 分组 | 频数 | 频率 |
 | 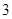 | 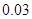 |
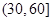 | 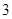 | 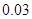 |
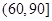 | 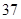 | 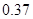 |
 | 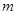 | 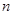 |
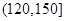 | 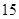 | 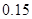 |
| 合计 | 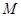 | 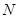 |
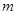 、
、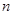 、
、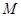 、
、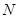 的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;
的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;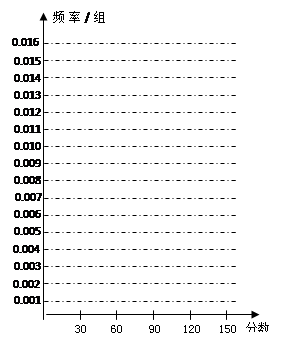
(2)若我区参加本次考试的学生有600人,试估计这次测试中我区成绩在
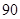 分以上的人数;
分以上的人数;(3)若该校教师拟从分数不超过60的学生中选取2人进行个案分析,求被选中2人分数不超过30分
的概率.
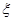 的分布列;
的分布列;  是从区间[0,3] 任 取 的一个数,
是从区间[0,3] 任 取 的一个数,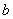 是从区间[0,2]任取的一个数,求上述方程有实根的概率.
是从区间[0,2]任取的一个数,求上述方程有实根的概率.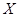 ,求
,求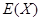 .
.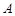 和
和 中装有若干个均匀的红球和白球,从
中装有若干个均匀的红球和白球,从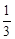 ,从
,从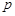 .
.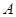 中有放回地摸球,每次摸出一个,共摸4次.
中有放回地摸球,每次摸出一个,共摸4次.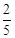 ,求
,求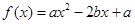 (
(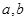
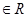 )
)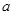 从集合
从集合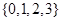 中任取一个元素,
中任取一个元素,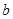 从集合
从集合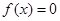 恰有两个不相等实根的概率;
恰有两个不相等实根的概率;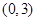 中任取一个数,
中任取一个数, 中任取一个数
中任取一个数