题目内容
已知函数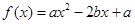 (
(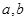
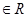 )
)
(1)若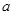 从集合
从集合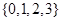 中任取一个元素,
中任取一个元素,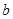 从集合
从集合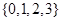 中任取一个元素,
中任取一个元素,
求方程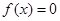 恰有两个不相等实根的概率;
恰有两个不相等实根的概率;
(2)若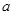 从区间
从区间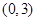 中任取一个数,
中任取一个数,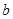 从区间
从区间 中任取一个数
中任取一个数
求方程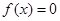 没有实根的概率.
没有实根的概率.
(1) (2)
(2)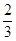
解析试题分析:(1) ∵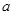 取集合
取集合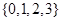 中任一个元素,
中任一个元素,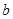 取集合{0,1,2,3}中任一个元素
取集合{0,1,2,3}中任一个元素 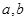 取值的情况是:
取值的情况是:


 ,(0,3),(1,3),(2,3),(3,3)其中第一个数表示
,(0,3),(1,3),(2,3),(3,3)其中第一个数表示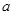 的取值,第二个数表示
的取值,第二个数表示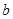 的取值.
的取值.
即基本事件总数为16 2分
设“方程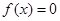 恰有两个不相等的实根”为事件
恰有两个不相等的实根”为事件 3分
3分
当 时,方程
时,方程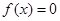 恰有两个不相等实根的充要条件为b>
恰有两个不相等实根的充要条件为b>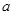 且
且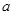 不等于零
不等于零
当b>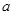 时,
时,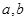 取值的情况有(1,2),(1,3),(2,3),
取值的情况有(1,2),(1,3),(2,3),
即 包含的基本事件数为3, 5分
包含的基本事件数为3, 5分
∴方程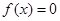 恰有两个不相等实根的概率
恰有两个不相等实根的概率 7分
7分
(2)∵若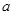 从区间
从区间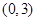 中任取一个数,
中任取一个数,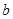 从区间
从区间 中任取一个数
中任取一个数
则试验的全部结果构成区域
这是一个矩形区域,其面积 9分
9分
设“方程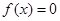 没有实根”为事件B, 10分
没有实根”为事件B, 10分
则事件B所构成的区域为
其面积
 12分
12分
由几何概型的概率计算公式可得:
方程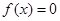 没有实根的概率
没有实根的概率 15分
15分
考点:古典概型概率与几何概型概率
点评:古典概型概率的求解主要是找到所有基本事件种数与满足题意要求的基本事件种数,然后求其比值;几何概型概率通常利用长度比,面积比体积比求解,在求解时首先要分析清楚属于哪种概率类型

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某工厂生产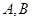 两种元件,其质量按测试指标划分为:大于或等于7.5为正品,小于7.5为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
两种元件,其质量按测试指标划分为:大于或等于7.5为正品,小于7.5为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
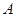 | 7 | 7 | 7.5 | 9 | 9.5 |
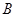 | 6 | 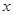 | 8.5 | 8.5 | 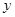 |
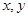 看不清,统计员只记得
看不清,统计员只记得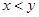 ,且
,且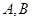 两种元件的检测数据的平均值相等,方差也相等.
两种元件的检测数据的平均值相等,方差也相等.(Ⅰ)求表格中
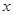 与
与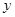 的值;
的值;(Ⅱ)若从被检测的5件
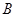 种元件中任取2件,求2件都为正品的概率.
种元件中任取2件,求2件都为正品的概率. 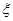 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求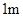 、
、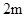 、
、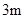 的钢管各
的钢管各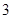 根(每根钢管质地均匀、粗细相同且附有不同的编号),从中随机抽取
根(每根钢管质地均匀、粗细相同且附有不同的编号),从中随机抽取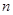 根(假设各钢管被抽取的可能性是均等的,
根(假设各钢管被抽取的可能性是均等的, ),再将抽取的钢管相接焊成笔直的一根.
),再将抽取的钢管相接焊成笔直的一根.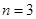 时,记事件
时,记事件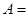 {抽取的
{抽取的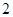 根长度相等},求
根长度相等},求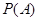 ;
;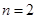 时,若用
时,若用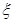 表示新焊成的钢管的长度(焊接误差不计),①求
表示新焊成的钢管的长度(焊接误差不计),①求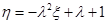 ,
,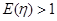 ,求实数
,求实数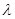 的取值范围.
的取值范围.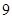 的
的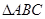 内任投一点
内任投一点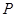 ,求
,求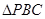 的面积小于
的面积小于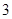 的概率?
的概率? (
(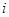 =1,2)表示方案
=1,2)表示方案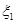 、
、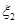 的分布列;
的分布列;