Question

【题目】在平面直角坐标系中，直线截以坐标原点为圆心的圆所得的弦长为.

（1）求圆的方程；

（2）若直线与圆切于第一象限，且与坐标轴交于点，，当时，求直线的方程；

（3）设，是圆上任意两点，点关于轴的对称点为，若直线，分别交轴于点和，问是否为定值？若是，请求出该定值；若不是，请说明理由.

Answer 1

【答案】（1）；（2）；（3）见解析

【解析】

（1）利用点到直线距离公式，可以求出弦心距，根据垂径定理结合勾股定理，可以求出圆的半径，进而可以求出圆的方程；

（2）设出直线的截距式方程，利用圆的切线性质，得到一个方程，结合已知，又得到一个方程，两个方程联立，解方程组，即可求出直线直线的方程；

（3）设，，则，，，分别求出直线与轴交点坐标、直线与轴交点坐标，求出的表达式，通过计算可得.

（1）因为点到直线的距离为，

所以圆的半径为，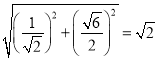

故圆的方程为.

（2）设直线的方程为，即，

由直线与圆相切，得，①

.②

由①②解得，

此时直线的方程为.

（3）设，，则，，，

直线与轴交点坐标为，，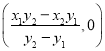

直线与轴交点坐标为，，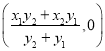

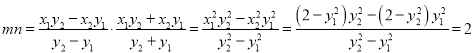，为定值2.