题目内容
将数列{(
)n-1}分组为:(1),(
,
),(
,
,
),(
,
,
,
),…,则第k组中的第一个数是 .
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 32 |
| 1 |
| 64 |
| 1 |
| 128 |
| 1 |
| 256 |
| 1 |
| 512 |
分析:根据分组的规律,计算出前k-1组中共含有项的个数即可求出第k组中的第一个数.
解答:解:根据分组规律可知,前k-1组共有1+2+3+…+(k-1)=
=
,
∴第k组中的第一个数为数列中的第
+1项,
∴第k组中的第一个数为(
)
+1-1=(
)
.
故答案为:(
)
.
| (k-1)(1+k-1) |
| 2 |
| k(k-1) |
| 2 |
∴第k组中的第一个数为数列中的第
| k(k-1) |
| 2 |
∴第k组中的第一个数为(
| 1 |
| 2 |
| k(k-1) |
| 2 |
| 1 |
| 2 |
| k(k-1) |
| 2 |
故答案为:(
| 1 |
| 2 |
| k(k-1) |
| 2 |
点评:本题主要考查等比数列的通项公式的应用,根据数列分组的规律确定前k-1组项的个数是解决本题的关键,考查学生的计算能力.

练习册系列答案
相关题目
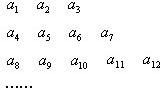 将数列{an}中的所有项按第一行排3项,以下每一行比上一行多一项的规则排成如下数表:
将数列{an}中的所有项按第一行排3项,以下每一行比上一行多一项的规则排成如下数表: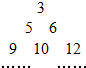 设an是集合2s+2t|0≤s<t,s,t∈Z中所有的数从小到大排列成的数列,即a1=3,a2=5,a3=6,a4=9,a5=10,a6=12,…,将数列an各项按照上小下大、左小右大的原则写成如下的三角形数表:
设an是集合2s+2t|0≤s<t,s,t∈Z中所有的数从小到大排列成的数列,即a1=3,a2=5,a3=6,a4=9,a5=10,a6=12,…,将数列an各项按照上小下大、左小右大的原则写成如下的三角形数表: 将数列{an}中的所有项按每一行比上一行多一项的规则排成如数表:记表中的第一列数a1,a2,a4,
将数列{an}中的所有项按每一行比上一行多一项的规则排成如数表:记表中的第一列数a1,a2,a4,