题目内容
5.若α是锐角三角形的一个内角,且cos($\frac{3}{2}$π+α)=$\frac{1}{3}$,则cosα=$\frac{2\sqrt{2}}{3}$.分析 由已知利用诱导公式可求sinα,利用同角三角函数基本关系式即可计算得解.
解答 解:∵α是锐角,cos($\frac{3}{2}$π+α)=cos(π+$\frac{π}{2}$+α)=sinα=$\frac{1}{3}$,
∴cosα=$\sqrt{1-si{n}^{2}α}$=$\sqrt{1-\frac{1}{9}}$=$\frac{2\sqrt{2}}{3}$.
故答案为:$\frac{2\sqrt{2}}{3}$.
点评 本题主要考查了诱导公式,同角三角函数基本关系式在三角函数化简求值中的应用,属于基础题.

练习册系列答案
相关题目
20.f(x)=xcosx-5sinx+2,若f(2)=7,则f(-2)的值为( )
| A. | -7 | B. | 9 | C. | -5 | D. | -3 |
15.执行如图的程序框图,输出S的值为( )
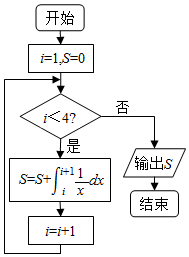

| A. | ln4 | B. | ln5 | C. | ln 5-ln4 | D. | ln 4-ln 3 |
 如图,已知在△ABC中,AC的中点为E,AB的中点为F,延长BE至P,使BE=EP,延长CF至Q,使CF=FQ.试用向量方法证明P,A,Q三点共线.
如图,已知在△ABC中,AC的中点为E,AB的中点为F,延长BE至P,使BE=EP,延长CF至Q,使CF=FQ.试用向量方法证明P,A,Q三点共线.