题目内容
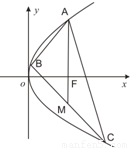
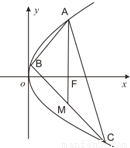
如图,已知点A(-4a,0)(a>0),B、C两点分别在y轴和x轴上运动,并且满足(1)求动点Q的轨迹方程;
(2)设过点A的直线与点Q的轨迹交于E、F两点,A′(4a,0),求直线A′E、A ′F的斜率之和.
解析:(1)设Q(x,y),因为![]() =
=![]()
![]() ,
,
所以B(0,-![]() ).
).
又A(-4a,0),所以![]() =(4a,-
=(4a,-![]() ),
),![]() =(x,
=(x,![]() ).
).
由已知![]() ·
·![]() =0,则4ax-
=0,则4ax-![]() y2=0,
y2=0,
y2=9ax,即Q点轨迹方程为y2=9ax;
(2)设过点A的直线为
y=k(x+4a)(k≠0),E(x1,y1),F(x2,y2)
由 ky2-9ay+36a2k=0(k≠0)
ky2-9ay+36a2k=0(k≠0)![]() y1y2=36a2,
y1y2=36a2,
kA′E+kA′F=![]()
=![]() .
.
又y12=9ax1,y22=9ax2,
所以kA′B+kA′F= ,
,
由y1y2=36a2,得kA′E+kA′F=0.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
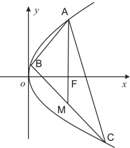 如图,已知点A(4,8),B(x1,y1),C(x2,y2)在抛物线y2=2px上,△ABC的重心与此抛物线的焦点F重合,M为 BC中点.
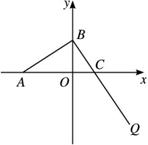
如图,已知点A(4,8),B(x1,y1),C(x2,y2)在抛物线y2=2px上,△ABC的重心与此抛物线的焦点F重合,M为 BC中点. 如图,已知点A(0,2)和抛物线y2=x+4上两点B、C,使得AB⊥BC,求点C的纵坐标的取值范围.
如图,已知点A(0,2)和抛物线y2=x+4上两点B、C,使得AB⊥BC,求点C的纵坐标的取值范围.