题目内容
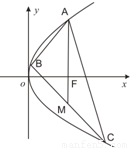
如图,已知点A(4,8),B(x1,y1),C(x2,y2)在抛物线y2=2px上,△ABC的重心与此抛物线的焦点F重合,M为 BC中点.(Ⅰ)求该抛物线的方程和焦点F的坐标;
(Ⅱ)求BC所在直线的方程.
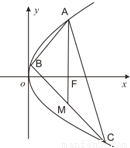
【答案】分析:(Ⅰ)将点A(4,8)代入抛物线y2=2px,解得p=8,求出方程及焦点.
(Ⅱ)利用重心的定义,得出M点的坐标为(4,-4),再利用差分法求BC所在直线的方程.
解答:解:(Ⅰ)由点A(4,8),在抛物线y2=2px上解得p=8,
∴抛物线的方程为y2=16x,焦点F的坐标(4,0)
(Ⅱ)∵△ABC的重心与此抛物线的焦点F重合
由B(x1,y1),C(x2,y2)得:
∴x1+x2=8,y1+y2=-8,M点的坐标为(4,-4)
由B,C在抛物线y2=16x上, 两方程作差y12-y22=16(x1-x2)
两方程作差y12-y22=16(x1-x2)
∴直线BC的斜率
∴BC所在直线的方程为y+4=-2(x-4),即2x+y-4=0
点评:本题考查抛物线的标准方程,直线方程求解.若知弦中点求弦所在直线方程时常用“差分法”求解.
(Ⅱ)利用重心的定义,得出M点的坐标为(4,-4),再利用差分法求BC所在直线的方程.
解答:解:(Ⅰ)由点A(4,8),在抛物线y2=2px上解得p=8,
∴抛物线的方程为y2=16x,焦点F的坐标(4,0)
(Ⅱ)∵△ABC的重心与此抛物线的焦点F重合
由B(x1,y1),C(x2,y2)得:

∴x1+x2=8,y1+y2=-8,M点的坐标为(4,-4)
由B,C在抛物线y2=16x上,
 两方程作差y12-y22=16(x1-x2)
两方程作差y12-y22=16(x1-x2)∴直线BC的斜率

∴BC所在直线的方程为y+4=-2(x-4),即2x+y-4=0
点评:本题考查抛物线的标准方程,直线方程求解.若知弦中点求弦所在直线方程时常用“差分法”求解.

练习册系列答案
相关题目
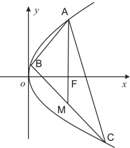 如图,已知点A(4,8),B(x1,y1),C(x2,y2)在抛物线y2=2px上,△ABC的重心与此抛物线的焦点F重合,M为 BC中点.
如图,已知点A(4,8),B(x1,y1),C(x2,y2)在抛物线y2=2px上,△ABC的重心与此抛物线的焦点F重合,M为 BC中点. 如图,已知点A(0,2)和抛物线y2=x+4上两点B、C,使得AB⊥BC,求点C的纵坐标的取值范围.
如图,已知点A(0,2)和抛物线y2=x+4上两点B、C,使得AB⊥BC,求点C的纵坐标的取值范围.