题目内容
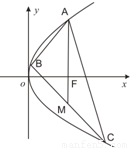
如图,已知点A(4,0),B(4,4),C(2,6),求AC和OP的交点P的坐标.
思路分析:方法一:设出P点坐标,利用![]() 与
与![]() 共线,
共线,![]() 与
与![]() 共线,列出方程组,通过解方程组求得P点坐标.
共线,列出方程组,通过解方程组求得P点坐标.
方法二:由![]() 与
与![]() 共线,用B点坐标表示P点坐标,然后利用
共线,用B点坐标表示P点坐标,然后利用![]() 与
与![]() 共线求解.
共线求解.
解法一:
设点P的坐标为(x,y),则![]() =(x,y),
=(x,y),![]() =(4,4).
=(4,4).
∵![]() 与
与![]() 共线,∴4x-4y=0.①
共线,∴4x-4y=0.①
又∵![]() =(x-4,y),
=(x-4,y),![]() =(-2,6),
=(-2,6),![]() 与
与![]() 共线,
共线,
∴6(x-4)+2y=0.②
由①②得x=3,y=3,∴P点坐标为(3,3).
解法二:设![]() =λ
=λ![]() =(4λ,4λ),则
=(4λ,4λ),则![]() =(4λ-4,4λ),
=(4λ-4,4λ),![]() =(-2,6),
=(-2,6),
∵![]() 与
与![]() 共线,∴24λ+8λ=24,λ=
共线,∴24λ+8λ=24,λ=![]() .
.
∴![]() =(3,3),即P点坐标为(3,3).
=(3,3),即P点坐标为(3,3).
温馨提示
本题主要考查向量的运算,以及点的坐标与向量的坐标间的转化,解法二利用共线条件设出了点的坐标,简化了运算.

练习册系列答案
相关题目
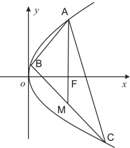 如图,已知点A(4,8),B(x1,y1),C(x2,y2)在抛物线y2=2px上,△ABC的重心与此抛物线的焦点F重合,M为 BC中点.
如图,已知点A(4,8),B(x1,y1),C(x2,y2)在抛物线y2=2px上,△ABC的重心与此抛物线的焦点F重合,M为 BC中点. 如图,已知点A(0,2)和抛物线y2=x+4上两点B、C,使得AB⊥BC,求点C的纵坐标的取值范围.
如图,已知点A(0,2)和抛物线y2=x+4上两点B、C,使得AB⊥BC,求点C的纵坐标的取值范围.