题目内容
若过点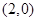 的直线与曲线
的直线与曲线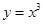 和
和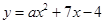 都相切,则
都相切,则 的值为( )
的值为( )
A.2或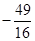 | B.3或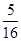 | C.2 | D.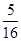 |
A
解析试题分析:设过曲线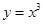 上的点
上的点 的切线过点
的切线过点 ,对函数
,对函数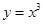 求导得
求导得 ,故曲线
,故曲线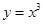 上的点
上的点 的切线方程为
的切线方程为 ,即
,即 ,将点
,将点 的坐标代入此切线方程得
的坐标代入此切线方程得 ,即
,即 ,解得
,解得 或
或 ,(1)当
,(1)当 时,则切线方程为
时,则切线方程为 ,即切线为
,即切线为 轴,此时曲线
轴,此时曲线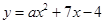 与
与 轴相切,则
轴相切,则 ;(2)当
;(2)当 时,切线的方程为
时,切线的方程为 ,对函数
,对函数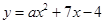 求导得
求导得 ,令
,令 ,则有
,则有
 ,解得
,解得 ,将
,将 代入
代入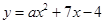 得
得 ,即切点坐标为
,即切点坐标为 代入切线方程得
代入切线方程得 ,化简得
,化简得 ,解得
,解得 ,综上所述
,综上所述 或
或 .
.
考点:函数图象的切线方程

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
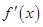 是函数
是函数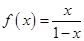 的导数,则
的导数,则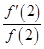 的值是( )
的值是( )
A.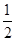 | B. | C.2 | D.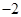 |
定义:符合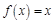 的
的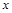 称为
称为 的一阶不动点,符合
的一阶不动点,符合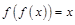 的
的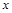 称为
称为 的二阶不动点。设函数
的二阶不动点。设函数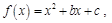 若函数
若函数 没有一阶不动点,则函数
没有一阶不动点,则函数 二阶不动点的个数为 ( )
二阶不动点的个数为 ( )
| A.四个 | B.两个 | C.一个 | D.零个 |
已知函数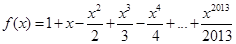 ,
,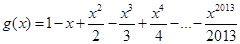 ,设函数
,设函数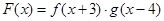 ,且函数
,且函数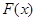 的零点均在区间
的零点均在区间 内,则
内,则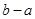 的最小值为( )
的最小值为( )
| A.11 | B.10 | C.9 | D.8 |
定义在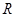 上的函数
上的函数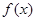 满足
满足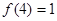 ,
,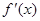 为
为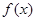 的导函数,已知
的导函数,已知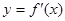 的图像如图所示,若两个正数
的图像如图所示,若两个正数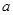 、
、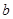 满足
满足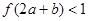 ,则
,则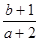 的取值范围是 ( )
的取值范围是 ( ) 
A.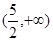 | B. | C.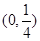 | D.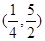 |
定义在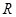 上的函数
上的函数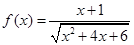 ,则
,则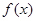 ( )
( )
| A.既有最大值也有最小值 | B.既没有最大值,也没有最小值 |
| C.有最大值,但没有最小值 | D.没有最大值,但有最小值 |
函数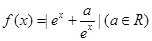 在区间
在区间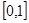 上单调递增,则
上单调递增,则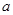 的取值范围是( )
的取值范围是( )
A.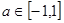 | B.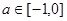 | C.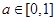 | D.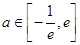 |
设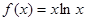 ,若
,若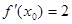 ,则
,则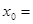 ( )
( )
A.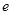 | B.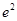 | C.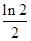 | D.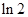 |
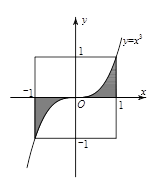
 是图中边长为2的正方形区域,
是图中边长为2的正方形区域,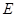 是函数
是函数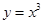 的图象与
的图象与 轴及
轴及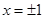 围成的阴影区域.向
围成的阴影区域.向