题目内容
已知过点(1,2)的二次函数y=ax2+bx+c的图象如图,给出下列论断:①abc>0,②a-b+c<0,③b<1,④ .其中正确论断是( )
.其中正确论断是( )
A.①③
B.②④
C.②③
D.②③④
【答案】分析:由已知中过点(1,2)的二次函数y=ax2+bx+c的图象,我们可以根据函数图象开口方向,对称轴,与坐标轴的交点位置等方向入手,构造不等式逐一判断题目中的四个结论,即可得到答案.
解答:解:∵函数图象的开口方向朝上,
∴a>0,
因为抛物线与y轴交于y轴负半轴,所以c<0,
对称轴x=- <0,所以b>0,
<0,所以b>0,
所以abc<0,所以①abc>0错误
当x=1时,函数值为2>0,所以②a+b+c=2对
当x=-1时,函数值<0,
即a-b+c<0,(1)
又a+b+c=2,
将a+c=2-b代入(1),
2-2b<0,
所以b>1
所以③b<1错误
因为对称轴x=- >-1,
>-1,
解得:a> ,
,
又因为b>1,
所以a> ,
,
所以④对
故选B
点评:本题考查的知识点是二次函数的性质,二次函数图象的开口方向、对称轴及顶点、与坐标轴的交点是处理二次函数问题常常要考虑的关键点.
解答:解:∵函数图象的开口方向朝上,
∴a>0,
因为抛物线与y轴交于y轴负半轴,所以c<0,
对称轴x=-
 <0,所以b>0,
<0,所以b>0,所以abc<0,所以①abc>0错误
当x=1时,函数值为2>0,所以②a+b+c=2对
当x=-1时,函数值<0,
即a-b+c<0,(1)
又a+b+c=2,
将a+c=2-b代入(1),
2-2b<0,
所以b>1
所以③b<1错误
因为对称轴x=-
 >-1,
>-1,解得:a>
 ,
,又因为b>1,
所以a>
 ,
,所以④对
故选B
点评:本题考查的知识点是二次函数的性质,二次函数图象的开口方向、对称轴及顶点、与坐标轴的交点是处理二次函数问题常常要考虑的关键点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
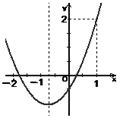 已知过点(1,2)的二次函数y=ax2+bx+c的图象如图,给出下列论断:①abc>0,②a-b+c<0,③b<1,④
已知过点(1,2)的二次函数y=ax2+bx+c的图象如图,给出下列论断:①abc>0,②a-b+c<0,③b<1,④ 已知过点(1,2)的二次函数y=ax2+bx+c的图象如图,给出下列论断:
已知过点(1,2)的二次函数y=ax2+bx+c的图象如图,给出下列论断:
 .其中正确论断是( )
.其中正确论断是( )