题目内容
如图所示,已知梯形ABCD中,AD∥BC,E、F分别是AD、BC边上的中点,且BC=3AD,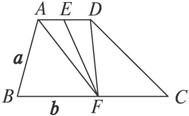
解:∵AD∥BC且AD=![]() BC,
BC,
∴![]() =
=![]()
![]() =
=![]() b.
b.
∴![]() =
=![]()
![]() =
=![]() b.
b.
又∵![]() =
=![]()
![]() ,
,
∴![]() =
=![]() b.
b.
∴![]() =
=![]() -
-![]() =a-
=a-![]() b.
b.
∴![]() =
=![]() +
+![]() =-
=-![]() -
-![]() =-
=-![]() b-(a-
b-(a-![]() b)=
b)=![]() b-a.
b-a.
![]() =
=![]() +
+![]() =
=![]() +
+![]() =-
=-![]() +
+![]() =-
=-![]() b+
b+![]() b-a=
b-a=![]() b-a.
b-a.
![]() =
=![]() +
+![]() =-(
=-(![]() +
+![]() )=-(
)=-(![]() b-a+
b-a+![]() b)=a-
b)=a-![]() b.
b.
温馨提示
(1)本例实质上是平面向量基本定理的应用,由于![]() 与
与![]() 不共线,因此,平面内的所有向量都可用它们表示出来.
不共线,因此,平面内的所有向量都可用它们表示出来.
(2)任一平面直线型图形,根据平面向量基本定理,都可以表示为某些向量的线性组合.这样解答几何问题,应先把已知和结论线段表示为向量形式,然后通过向量的运算,达到解决问题的目的.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 ,
, ,试用a,b表示
,试用a,b表示 、
、 、
、 .
.
 ,
, ,试用a、b为基底表示
,试用a、b为基底表示 、
、 、
、 .
.
 ,
, ,试用a,b表示
,试用a,b表示 、
、 、
、 .
.
 时,求双曲线的离心率e的取值范围.
时,求双曲线的离心率e的取值范围.

