题目内容
11．设α是第二象限角，P（x，4）为其终边上一点，且$cosα=\frac{1}{5}x$，则x=-3，tanα=-$\frac{4}{3}$．分析 由条件利用任意角的三角函数的定义，求得x的值，可得tanα的值．
解答 解：∵α是第二象限角，P（x，4）为其终边上的一点，∴x＜0，
∵cosα=$\frac{x}{5}$=$\frac{x}{\sqrt{{x}^{2}+16}}$，
∴x=-3，
∴tanα=-$\frac{4}{3}$，
故答案为：-3，-$\frac{4}{3}$
点评 本题主要考查任意角的三角函数的定义，属于基础题．
练习册系列答案
激活思维智能训练课时导学练系列答案
相关题目
1．
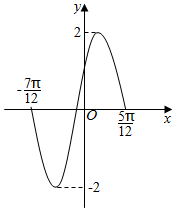已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的部分图象如图所示，则下列判断错误的是（ ）
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的部分图象如图所示，则下列判断错误的是（ ）| A． | A=2 | B． | ω=2 | C． | f（0）=1 | D． | φ=$\frac{5π}{6}$ |
已知椭圆C1：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的离心率为$\frac{{\sqrt{2}}}{2}$，其短轴的下端点在抛物线x2=4y的准线上．
19．
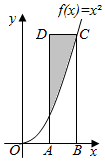如图，点A的坐标为（1，0），点C的坐标为（2，4），函数f（x）=x2，四边形ABCD是矩形，则阴影区域的面积等于（ ）
如图，点A的坐标为（1，0），点C的坐标为（2，4），函数f（x）=x2，四边形ABCD是矩形，则阴影区域的面积等于（ ）| A． | $\frac{4}{3}$ | B． | $\frac{5}{3}$ | C． | 2 | D． | $\frac{7}{3}$ |
3．为了解某地区某种农产品的年产量x（单位：吨）对价格y（单位：千元/吨）和利润z的影响，对近五年该农产品的年产量和价格统计如表：
（Ⅰ）求y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$；
（Ⅱ）若每吨该农产品的成本为2千元，假设该农产品可全部卖出，预测当年产量为多少时，年利润z取到最大值？（保留两位小数）
参考公式：$\widehat{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}（{x}_{i}{y}_{i}）-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$．
| x | 1 | 2 | 3 | 4 | 5 |
| y | 7.0 | 6.5 | 5.5 | 3.8 | 2.2 |
（Ⅱ）若每吨该农产品的成本为2千元，假设该农产品可全部卖出，预测当年产量为多少时，年利润z取到最大值？（保留两位小数）
参考公式：$\widehat{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}（{x}_{i}{y}_{i}）-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$．