题目内容
若直线y=kx+1（k∈R）与双曲线x2-y2=1有一个公共点，求实数k的取值集合________．
{
，-
，，
}
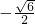分析：由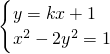
，消去y得（1-2k2）x2-4kx-3=0．若1-2k2≠0，则△=（4k）2-4（1-2k2）（-3）=0，得k=±．若1-2k2=0，得k=±．由此能求出实数k的取值的集合．
解答：由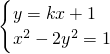，消去y得（1-2k2）x2-4kx-3=0．
若1-2k2≠0，则△=（4k）2-4（1-2k2）（-3）=0，得k=±．
若1-2k2=0，得k=±．
当k=时，得交点坐标为（-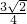
，
）；
当k=-时，得交点坐标为（，），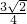
∴实数k的取值的集合是：{，-，，}．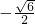
故答案为：{，-，，}．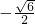
点评：本题主要考查直线与圆锥曲线的综合应用能力，具体涉及到直线与双曲线的相关知识，解题时要注意合理地进行等价转化．
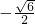，-，，}分析：由
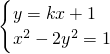，消去y得（1-2k2）x2-4kx-3=0．若1-2k2≠0，则△=（4k）2-4（1-2k2）（-3）=0，得k=±．若1-2k2=0，得k=±．由此能求出实数k的取值的集合．解答：由
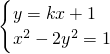，消去y得（1-2k2）x2-4kx-3=0．若1-2k2≠0，则△=（4k）2-4（1-2k2）（-3）=0，得k=±
．若1-2k2=0，得k=±
．当k=
时，得交点坐标为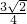（-，）；当k=-
时，得交点坐标为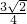（，），∴实数k的取值的集合是：{
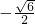，-，，}．故答案为：{
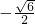，-，，}．点评：本题主要考查直线与圆锥曲线的综合应用能力，具体涉及到直线与双曲线的相关知识，解题时要注意合理地进行等价转化．
练习册系列答案
相关题目