题目内容
|
|<
的解集为A,关于x的不等式|x-1|+|x+2|>a的解集为B,且A?B,则实数a的取值范围为
| 1 |
| x-1 |
| 1 |
| 5 |
a≤7
a≤7
.分析:先解绝对值不等式|
|<
得出集合A={x|x<-4或x>6}.设y=|x-1|+|x+2|和y=a,分别画出这两个函数的图象,如图.要使得A?B,结合图象实数a的取值范围即可.
| 1 |
| x-1 |
| 1 |
| 5 |
解答: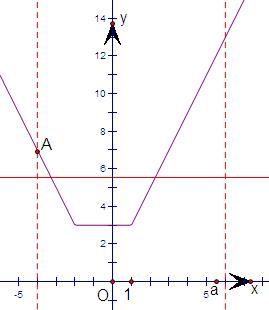 解:∵|
解:∵|
|<
⇒|x|>5⇒x<-4或x>6.
设y=|x-1|+|x+2|和y=a,分别画出这两个函数的图象,如图.
要使得A?B,结合图象知:
实数a的取值范围为:a≤7.
故答案为:a≤7.
 解:∵|
解:∵|| 1 |
| x-1 |
| 1 |
| 5 |
设y=|x-1|+|x+2|和y=a,分别画出这两个函数的图象,如图.
要使得A?B,结合图象知:
实数a的取值范围为:a≤7.
故答案为:a≤7.
点评:本小题主要考查集合关系中的参数取值问题、绝对值不等式、不等式的解法等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
相关题目
