题目内容
设f(x)的定义域是(-∞,0)∪(0,+∞),且f(x)对任意不为零的实数x都满足f(-x)=-f(x).已知当x>0时f(x)=| x |
| 1-2x |
(1)求当x<0时,f(x)的解析式 (2)解不等式f(x)<-
| x |
| 3 |
分析:(1)求当x<0时,f(x)的解析式,在哪个区间上求解析式,就在哪个区间上取值x,再转化到已知区间上求解析式,由f(-x)=-f(x)解出f(x)即可.
(2)解不等式f(x)<-
,分x>0和x<0两种情况,根据求得的解析式求解即可.
(2)解不等式f(x)<-
| x |
| 3 |
解答:解:(1)当x<0时,-x>0,f(-x)=
=
又f(-x)=-f(x)
所以,当x<0时,f(x)=
(2)x>0时,f(x)=
<-
,∴
<-
化简得∴
<0,解得1<2x<4∴0<x<2
当x<0时,
<-
∴
>0解得2x>1(舍去)或2x<
∴x<-2
解集为{x|x<-2或0<x<2}
| -x |
| 1-2-x |
| -x2x |
| 2x-1 |
所以,当x<0时,f(x)=
| x•2x |
| 2x-1 |
(2)x>0时,f(x)=
| x |
| 1-2x |
| x |
| 3 |
| 1 |
| 1-2x |
| 1 |
| 3 |
化简得∴
| 4-2x |
| 3(1-2x) |
当x<0时,
| x2x |
| 2x-1 |
| x |
| 3 |
4(2x-
| ||
| 3(2x-1) |
| 1 |
| 4 |
∴x<-2
解集为{x|x<-2或0<x<2}
点评:本题考查分段函数解析式的求法,注意在哪个区间上求解析式,就在哪个区间上取值,再转化到已知的区间上求解析式,再根据奇偶性,解出f(x)来.解不等式也要分段求解,注意x的取值范围.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
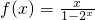
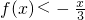 .
.
 .
.