题目内容
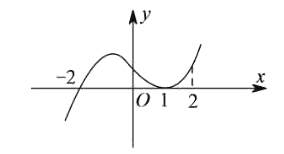
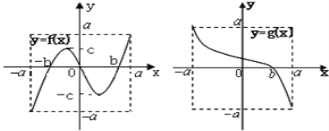
【题目】已知函数![]() ,
,![]() .
.
![]() 若
若![]() 是函数
是函数![]() 的极值点,求曲线
的极值点,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
![]() 若函数
若函数![]() 在区间
在区间![]() 上为单调递减函数,求实数a的取值范围;
上为单调递减函数,求实数a的取值范围;
![]() 设m,n为正实数,且
设m,n为正实数,且![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析
;(3)见解析
【解析】
![]() 求出导函数,得到函数
求出导函数,得到函数![]() 的极值点,解得
的极值点,解得![]() ,求出切线的斜率为
,求出切线的斜率为![]() ,切点为
,切点为![]() ,然后利用点斜式求解切线方程;
,然后利用点斜式求解切线方程;![]() 由
由![]() 知
知![]() ,利用函数
,利用函数![]() 在区间
在区间![]() 上为单调递减函数,得到
上为单调递减函数,得到![]() 在区间
在区间![]() 上恒成立,推出
上恒成立,推出![]() ,设
,设![]() ,
,![]() ,
,![]() ,利用基本不等式
,利用基本不等式![]() ,再求出函数的最大值,可得实数
,再求出函数的最大值,可得实数![]() 的取值范围;
的取值范围;![]() 利用分析法证明,要证
利用分析法证明,要证![]() ,只需证
,只需证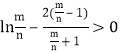 ,设
,设![]() ,
,![]() ,利用导数研究函数的单调性,可得
,利用导数研究函数的单调性,可得![]() ,从而可得结论.
,从而可得结论.
![]() ,
,![]() .
.
![]()
![]() 是函数
是函数![]() 的极值点,
的极值点,![]() ,解得
,解得![]() ,
,
经检验,当![]() 时,
时,![]() 是函数
是函数![]() 的极小值点,符合题意
的极小值点,符合题意![]()
此时切线的斜率为![]() ,切点为
,切点为![]() ,
,
则所求切线的方程为![]()
![]() 由
由![]() 知
知![]()
因为函数![]() 在区间
在区间![]() 上为单调递减函数,
上为单调递减函数,
所以不等式![]() 在区间
在区间![]() 上恒成立
上恒成立![]()
即![]() 在区间
在区间![]() 上恒成立,
上恒成立,
当![]() 时,由
时,由![]() 可得
可得![]() ,
,
设![]() ,
,![]() ,
,![]() ,
,
当且仅当![]() 时,即
时,即![]() 时,
时,![]() ,
,
又因为函数![]() 在区间
在区间![]() 上为单调递减,在区间
上为单调递减,在区间![]() 上为单调递增,
上为单调递增,
且![]() ,
,![]() ,
,
所以当![]() 时,
时,![]() 恒成立,
恒成立,
即![]() ,也即
,也即![]()
则所求实数a的取值范围是![]()
![]() ,n为正实数,且
,n为正实数,且![]() ,
,![]() 要证
要证![]() ,只需证
,只需证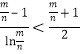
即证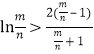 只需证
只需证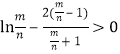
设![]() ,
,![]() ,
,
则![]() 在
在![]() 上恒成立,
上恒成立,
即函数![]() 在
在![]() 上是单调递增,
上是单调递增,
又![]() ,
,![]() ,即
,即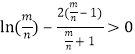 成立,
成立,
也即![]() 成立.
成立.

【题目】甲、乙两台机床同时生产一种零件,其质量按测试指标划分:指标大于或等于100为优品,大于等于90且小于100为合格品,小于90为次品,现随机抽取这两台机床生产的零件各100件进行检测,检测结果统计如下:
测试指标 | [85,90) | [90,95) | [95,100) | [100,105) | [105,110) |
甲机床 | 8 | 12 | 40 | 32 | 8 |
乙机床 | 7 | 18 | 40 | 29 | 6 |
(1)试分别估计甲机床、乙机床生产的零件为优品的概率;
(2)甲机床生产1件零件,若是优品可盈利160元,合格品可盈利100元,次品则亏损20元,假设甲机床某天生产50件零件,请估计甲机床该天的利润(单位:元);
(3)从甲、乙机床生产的零件指标在[90,95)内的零件中,采用分层抽样的方法抽取5件,从这5件中任意抽取2件进行质量分析,求这2件都是乙机床生产的概率.