题目内容
已知f(n)=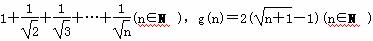 .
.
(1) 当n=1,2,3时,分别比较f(n)与g(n)的大小(直接给出结论);
(2) 由(1)猜想f(n)与g(n)的大小关系,并证明你的结论.
解:(1) 当n=1时,f(1)>g(1);
当n=2时,f(2)>g(2);
当n=3时,f(3)>g(3).
(2) 猜想:f(n)>g(n)(n∈N*),即 (n∈N*).
(n∈N*).
下面用数学归纳法证明:
①当n=1时,f(1)=1,g(1)=2(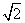 -1),f(1)>g(1).
-1),f(1)>g(1).
②假设当n=k时,猜想成立,即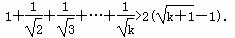
则当n=k+1时,f(k+1)=
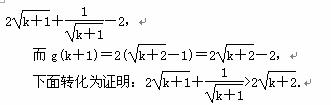
只要证:2(k+1)+1=2k+3>2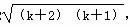 ,
,
需证:(2k+3)2>4(k+2)(k+1),
即证:4k2+12k+9>4k2+12k+8,此式显然成立.
所以,当n=k+1时猜想也成立.
综上可知:对n∈N*,猜想都成立,
即 (n∈N*)成立.
(n∈N*)成立.

练习册系列答案
相关题目
 =1的渐近线方程为________.
=1的渐近线方程为________. ”时,假设的内容应为______________.
”时,假设的内容应为______________. +
+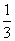 +…+
+…+ (n∈N),则n=1时,f(n)=________.
(n∈N),则n=1时,f(n)=________. ,试比较f(n)与
,试比较f(n)与 的大小.
的大小. n(n+1)(2n+1)(n∈N*)”,当n=k+1时,应在n=k时的等式左边添加的项是________.
n(n+1)(2n+1)(n∈N*)”,当n=k+1时,应在n=k时的等式左边添加的项是________. 的值为6,那么运行相应程序,输出的
的值为6,那么运行相应程序,输出的 的值为
的值为
 中,已知
中,已知 ,则
,则 等于
等于 (B)
(B) (C)
(C) (D)
(D)
 的精美卡片,每瓶酒酒盒随机装入一张卡片,集齐3种卡片可获奖,现购买该种酒5瓶,能获奖的概率为________.
的精美卡片,每瓶酒酒盒随机装入一张卡片,集齐3种卡片可获奖,现购买该种酒5瓶,能获奖的概率为________.