题目内容
 如图,直线与圆x2+y2=1分别在第一和第二象限内交于P1,P2两点,若点P1的横坐标为
如图,直线与圆x2+y2=1分别在第一和第二象限内交于P1,P2两点,若点P1的横坐标为| 3 |
| 5 |
| π |
| 3 |
3-4
| ||
| 10 |
3-4
| ||
| 10 |
分析:利用圆的方程,点P1的横坐标,求出∠XOP1的正弦函数与余弦函数,通过两角和的正弦函数求出P2的横坐标即可.
解答:解:因为直线与圆x2+y2=1分别在第一和第二象限内交于P1,P2两点,若点P1的横坐标为
,
所以cos∠XOP1=
,sin∠XOP1=
,又∠P1OP2=
,
所以cos(∠XOP1+
)=cos∠XOP1cos
-sin∠XOP1sin
=
×
-
×
=
.
所以P2的横坐标为:
.
故答案为:
.
| 3 |
| 5 |
所以cos∠XOP1=
| 3 |
| 5 |
| 4 |
| 5 |
| π |
| 3 |
所以cos(∠XOP1+
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
=
| 3 |
| 5 |
| 1 |
| 2 |
| 4 |
| 5 |
| ||
| 2 |
=
3-4
| ||
| 10 |
所以P2的横坐标为:
3-4
| ||
| 10 |
故答案为:
3-4
| ||
| 10 |
点评:本题考查任意角的三角函数的定义,两角和与差的余弦函数,考查计算能力.

练习册系列答案
相关题目
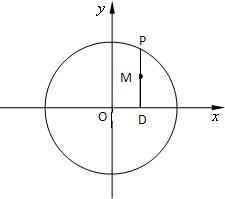 如图,P是圆x2+y2=4上的动点,P点在x轴上的投影是D,点M满足
如图,P是圆x2+y2=4上的动点,P点在x轴上的投影是D,点M满足
 如图,直线与圆x2+y2=1分别在第一和第二象限内交于P1,P2两点,若点P1的横坐标为
如图,直线与圆x2+y2=1分别在第一和第二象限内交于P1,P2两点,若点P1的横坐标为 ,∠P1OP2=
,∠P1OP2= ,则点P2的横坐标为________.
,则点P2的横坐标为________.