题目内容
(本小题满分12分)
设二次函数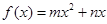 ,函数
,函数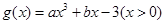 ,且有
,且有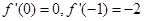 ,
,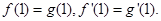
(1)求函数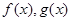 的解析式;
的解析式;
(2)是否存在实数k和p,使得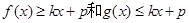 成立,若存在,求出k和p的值;若不存在,说明理由.
成立,若存在,求出k和p的值;若不存在,说明理由.
设二次函数
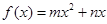 ,函数
,函数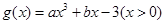 ,且有
,且有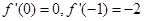 ,
,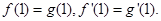
(1)求函数
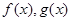 的解析式;
的解析式;(2)是否存在实数k和p,使得
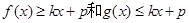 成立,若存在,求出k和p的值;若不存在,说明理由.
成立,若存在,求出k和p的值;若不存在,说明理由.(1)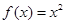
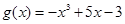 (
(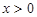 )
)
(2)
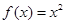
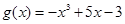 (
(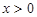 )
)(2)

(I)由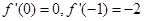 ,
,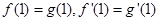 可建立关于a,b,m,n
可建立关于a,b,m,n
的方程,从而求出f(x),g(x)的解析式.
(2)假设存在,令f(x)=g(x)=kx+p,即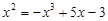 ,然后可以构造
,然后可以构造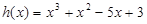 (
(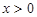 ),证明h(x)与x轴的正半轴有交点即可.然后再根据图像确定直线方程y=kx+p应满足什么条件.
),证明h(x)与x轴的正半轴有交点即可.然后再根据图像确定直线方程y=kx+p应满足什么条件.
(Ⅰ)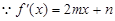 ,
,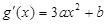 ,
,
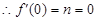 ,
, ,即
,即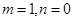 ,
,
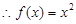 . (2分)
. (2分)
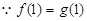 ,
,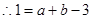 .
.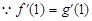 ,
, 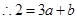 ,
,
解得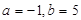 ,
, (
(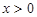 ). (4分)
). (4分)
(Ⅱ)令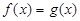 ,可得
,可得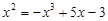 (
(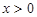 ).
).
(法一)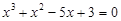 ,
, 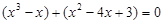 ,
,
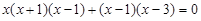 ,
,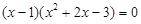 ,
,
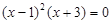 ,
, ,
, ,
,
即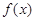 与
与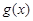 有且仅有一个交点为
有且仅有一个交点为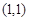 ,
,
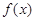 在点
在点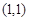 处的切线为
处的切线为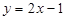 . (8分)
. (8分)
(法二)设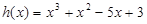 (
(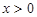 ),
),
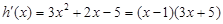 (
(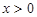 ),
),
令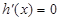 ,解得
,解得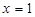 ,
,
且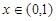 时,
时,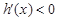 ,
, 单调递减,
单调递减,
 时,
时,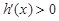 ,
, 单调递增,
单调递增,
 时,
时,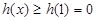 .
.
所以,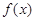 与
与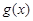 有且仅有一个交点为
有且仅有一个交点为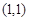 .
.
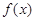 在点
在点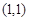 处的切线为
处的切线为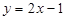 . (8分)
. (8分)
下面证明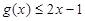 .
.
设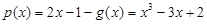 (
(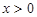 ),
),
(法一)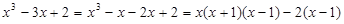
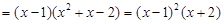
 ,
,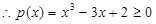 ,即
,即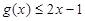 . (12分)
. (12分)
(法二)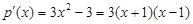 ,令
,令 ,解得
,解得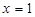 .
.
且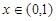 时,
时,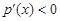 ,
,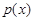 单调递减,
单调递减,
 时,
时,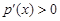 ,
,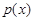 单调递增,
单调递增,
 时,
时,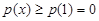 ,即
,即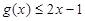 . (12分)
. (12分)
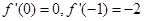 ,
,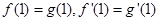 可建立关于a,b,m,n
可建立关于a,b,m,n的方程,从而求出f(x),g(x)的解析式.
(2)假设存在,令f(x)=g(x)=kx+p,即
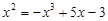 ,然后可以构造
,然后可以构造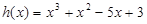 (
(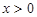 ),证明h(x)与x轴的正半轴有交点即可.然后再根据图像确定直线方程y=kx+p应满足什么条件.
),证明h(x)与x轴的正半轴有交点即可.然后再根据图像确定直线方程y=kx+p应满足什么条件.(Ⅰ)
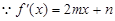 ,
,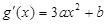 ,
,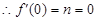 ,
, ,即
,即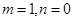 ,
,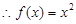 . (2分)
. (2分)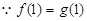 ,
,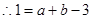 .
.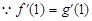 ,
, 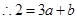 ,
,解得
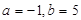 ,
, (
(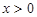 ). (4分)
). (4分)(Ⅱ)令
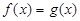 ,可得
,可得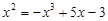 (
(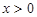 ).
).(法一)
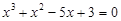 ,
, 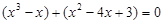 ,
,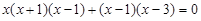 ,
,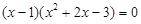 ,
,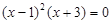 ,
, ,
, ,
,即
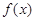 与
与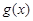 有且仅有一个交点为
有且仅有一个交点为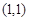 ,
,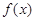 在点
在点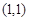 处的切线为
处的切线为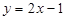 . (8分)
. (8分)(法二)设
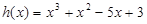 (
(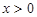 ),
),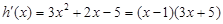 (
(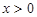 ),
),令
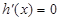 ,解得
,解得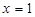 ,
,且
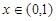 时,
时,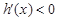 ,
, 单调递减,
单调递减, 时,
时,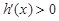 ,
, 单调递增,
单调递增, 时,
时,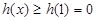 .
.所以,
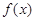 与
与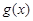 有且仅有一个交点为
有且仅有一个交点为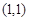 .
.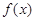 在点
在点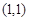 处的切线为
处的切线为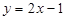 . (8分)
. (8分)下面证明
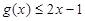 .
.设
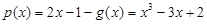 (
(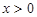 ),
),(法一)
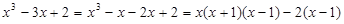
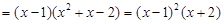
 ,
,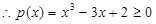 ,即
,即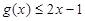 . (12分)
. (12分)(法二)
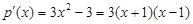 ,令
,令 ,解得
,解得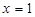 .
.且
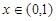 时,
时,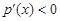 ,
,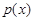 单调递减,
单调递减, 时,
时,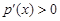 ,
,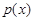 单调递增,
单调递增, 时,
时,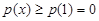 ,即
,即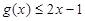 . (12分)
. (12分)
练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
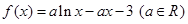 ,
,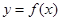 在点
在点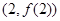 处的切线斜率为1,求
处的切线斜率为1,求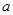 的值;
的值;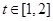 ,函数
,函数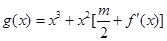 在区间
在区间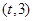 总存在极值,求
总存在极值,求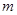 的取值范围;
的取值范围;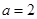 ,对于函数
,对于函数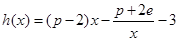 在
在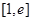 上至少存在一个
上至少存在一个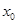 使得
使得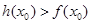 成立,求实数
成立,求实数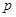 的取值范围。
的取值范围。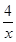 在点p(1,4)处的切线与直线l平行且距离为
在点p(1,4)处的切线与直线l平行且距离为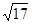 ,则直线l的方程为( )
,则直线l的方程为( )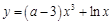 存在垂直于
存在垂直于 轴的切线,函数
轴的切线,函数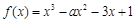 在
在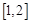 上单调递增,则
上单调递增,则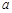 的范围为 .
的范围为 . 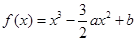 ,
,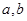 为实数,
为实数,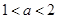 .
. 在区间
在区间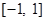 上的最小值、最大值分别为
上的最小值、最大值分别为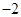 、1,求
、1,求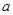 、
、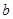 的值;
的值;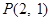 且与曲线
且与曲线 的方程;
的方程;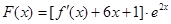 ,试判断函数
,试判断函数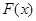 的极值点个数.
的极值点个数. 的图象在点
的图象在点 处的切线的倾斜角为
处的切线的倾斜角为



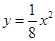 的一条切线的斜率为
的一条切线的斜率为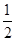 ,则切点的横坐标为( )
,则切点的横坐标为( )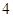
 =
=


