题目内容
【题目】已知函数f(x)=![]() cos(2x-
cos(2x-![]() ).
).
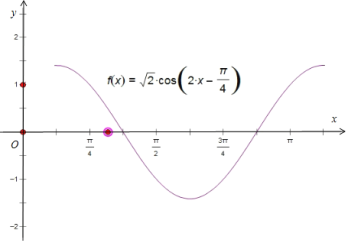
(1)利用“五点法”,完成以下表格,并画出函数f(x)在一个周期上的图象;
(2)求函数f(x)的单调递减区间和对称中心的坐标;
(3)如何由y=cosx的图象变换得到f(x)的图象.
2x- | 0 |
| π |
| 2π |
x | |||||
f(x) |
【答案】(1)详见解析(2)f(x)的单调减区间为:(![]() +kπ,
+kπ,![]() +kπ),k∈Z,对称中心为(
+kπ),k∈Z,对称中心为(![]() +
+![]() ,0),k∈Z;(3)详见解析
,0),k∈Z;(3)详见解析
【解析】
(1)利用“五点法”作出函数f(x)在一个周期上的图象(先列表,再画图);(2)利用余弦函数的单调性和对称性即可得解.(3)由条件利用y=Acos(ωx+φ)的图象变换规律,得出结论.
(1)列表如下:
2x- | 0 |
| π |
| 2π |
x |
|
|
|
|
|
f(x) |
| 0 | - | 0 |
|
画图如下:
(2)令2kπ<2x-![]() <π+2kπ,k∈Z,得:
<π+2kπ,k∈Z,得:![]() +kπ<x<
+kπ<x<![]() +kπ,k∈Z,
+kπ,k∈Z,
∴f(x)的单调减区间为:(![]() +kπ,
+kπ,![]() +kπ),k∈Z,
+kπ),k∈Z,
令2x-![]() =
=![]() +kπ,k∈Z,得:x=
+kπ,k∈Z,得:x=![]() +
+![]() ,k∈Z,
,k∈Z,
∴f(x)的对称中心为(![]() +
+![]() ,0),k∈Z,
,0),k∈Z,
(3)图象先向右平移![]() 个单位长度再纵坐标不变,横坐标缩小为原来的
个单位长度再纵坐标不变,横坐标缩小为原来的![]() 倍,最后横坐标不变,纵坐标伸长为原来的
倍,最后横坐标不变,纵坐标伸长为原来的![]() 倍
倍

练习册系列答案
相关题目