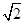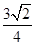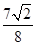题目内容
极坐标系中,由三条曲线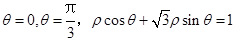 围成的图形的面积是( )
围成的图形的面积是( )
A.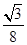 | B.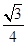 | C.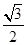 | D.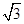 |
A
解析试题分析:将极坐标方程化为直角坐标方程为 ,
, ,
, ,直线
,直线 与
与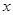 轴的交点为(1,0),与
轴的交点为(1,0),与 的交点为(
的交点为( ,
,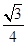 ),所以这三条曲线围成图形为顶点为(0,0),(
),所以这三条曲线围成图形为顶点为(0,0),( ,
,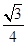 ),(1,0)的三角形,其的面积为
),(1,0)的三角形,其的面积为 =
=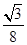 ,故选A.
,故选A.
考点:极坐标方程与直角坐标方程互化;两直线的交点;三角形面积公式

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
在平面直角坐标系中,曲线C: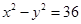 经过伸缩变换
经过伸缩变换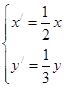 后,所得曲线的焦点坐标为( ).
后,所得曲线的焦点坐标为( ).
A.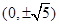 | B.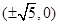 | C.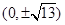 | D.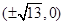 |
曲线的极坐标方程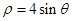 化为直角坐标为( )
化为直角坐标为( )
A. | B.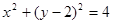 |
C.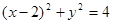 | D.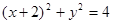 |
在极坐标系中,点 到直线
到直线 的距离等于( ).
的距离等于( ).
A.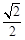 | B.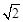 | C. | D.2 |
极坐标系中,以(9, )为圆心,9为半径的圆的极坐标方程为( )
)为圆心,9为半径的圆的极坐标方程为( )
A. | B. |
C. | D. |
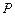 是圆
是圆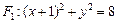 上任意一点,点
上任意一点,点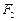 与点
与点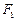 关于原点对称。线段
关于原点对称。线段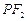 的中垂线
的中垂线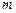 分别与
分别与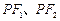 交于
交于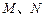 两点.
两点.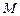 的轨迹
的轨迹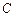 的方程;
的方程; 的直线
的直线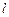 与曲线
与曲线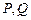 两点,若
两点,若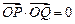 (
(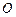 为坐标原点),试求直线
为坐标原点),试求直线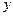 轴
轴 上截距的取值范围.
上截距的取值范围. 过点A(a,0),B(0,b)的直
过点A(a,0),B(0,b)的直 ,原点到该直线的距离为
,原点到该直线的距离为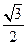 .
.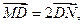 求直线MN的方程;
求直线MN的方程; 交椭圆于P、Q两点,以PQ为直径的圆过点D(1,0)?若存在,求出k的值;若不存在,请说明理由。
交椭圆于P、Q两点,以PQ为直径的圆过点D(1,0)?若存在,求出k的值;若不存在,请说明理由。 轴的非负半轴为极轴建立极坐标系,则线段
轴的非负半轴为极轴建立极坐标系,则线段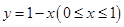 的极坐标为( )
的极坐标为( )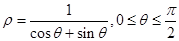
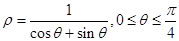


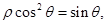 曲线C2的参数方程为
曲线C2的参数方程为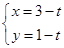 (
(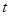 为参数),以极点为原点,极轴为
为参数),以极点为原点,极轴为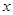 轴正半轴建立平面直角坐标系,则曲线C1上的点与曲线C2上的点最近的距离为
轴正半轴建立平面直角坐标系,则曲线C1上的点与曲线C2上的点最近的距离为