题目内容
如图所示,在直角梯形ABCD中,∠B=90°,DC∥AB,CD= AB,G为线段AB的中点,将△ADG沿GD折起,使平面ADG⊥平面BCDG,得到几何体A-BCDG,
AB,G为线段AB的中点,将△ADG沿GD折起,使平面ADG⊥平面BCDG,得到几何体A-BCDG,
(1)若E,F分别为线段AC,AD的中点,求证:EF∥平面ABG;
(2)求证:AG⊥平面BCDG。
 AB,G为线段AB的中点,将△ADG沿GD折起,使平面ADG⊥平面BCDG,得到几何体A-BCDG,
AB,G为线段AB的中点,将△ADG沿GD折起,使平面ADG⊥平面BCDG,得到几何体A-BCDG,(1)若E,F分别为线段AC,AD的中点,求证:EF∥平面ABG;
(2)求证:AG⊥平面BCDG。

证明:(1)依题意,折叠前后CD、BG的位置关系不改变,
∴CD∥BG,
∵E、F分别为线段AC、AD的中点,
∴在△ACD中,EF∥CD,∴EF∥BG,
又EF 平面ABG,BG
平面ABG,BG 平面ABG,
平面ABG,
∴EF∥平面ABG。
(2)将△ADG沿GD折起后,AG、GD的位置关系不改变,
∴AG⊥GD,
又平面ADG⊥平面BCDG,平面ADG∩平面BCDG=GD,AG 平面AGD,
平面AGD,
∴AG⊥平面BCDG。
∴CD∥BG,
∵E、F分别为线段AC、AD的中点,
∴在△ACD中,EF∥CD,∴EF∥BG,
又EF
 平面ABG,BG
平面ABG,BG 平面ABG,
平面ABG,∴EF∥平面ABG。
(2)将△ADG沿GD折起后,AG、GD的位置关系不改变,
∴AG⊥GD,
又平面ADG⊥平面BCDG,平面ADG∩平面BCDG=GD,AG
 平面AGD,
平面AGD,∴AG⊥平面BCDG。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
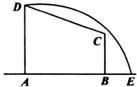 如图所示,在直角梯形ABCD中,|AD|=3,|AB|=4,|BC|=
如图所示,在直角梯形ABCD中,|AD|=3,|AB|=4,|BC|=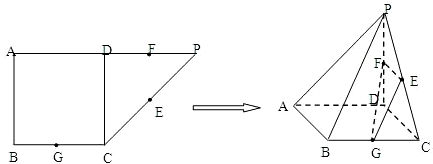
 如图所示,在直角梯形OABC中,
如图所示,在直角梯形OABC中,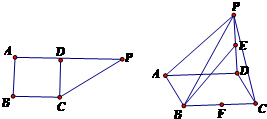 如图所示,在直角梯形ABCP中,AP∥BC,AB⊥AP,AB=BC=3,AP=7,CD⊥AP,现将△PCD沿折线CD折成直二面角P-CD-A,设E,F分别是PD,BC的中点.
如图所示,在直角梯形ABCP中,AP∥BC,AB⊥AP,AB=BC=3,AP=7,CD⊥AP,现将△PCD沿折线CD折成直二面角P-CD-A,设E,F分别是PD,BC的中点.