题目内容
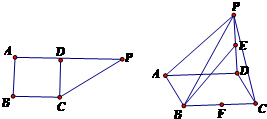 如图所示,在直角梯形ABCP中,AP∥BC,AB⊥AP,AB=BC=3,AP=7,CD⊥AP,现将△PCD沿折线CD折成直二面角P-CD-A,设E,F分别是PD,BC的中点.
如图所示,在直角梯形ABCP中,AP∥BC,AB⊥AP,AB=BC=3,AP=7,CD⊥AP,现将△PCD沿折线CD折成直二面角P-CD-A,设E,F分别是PD,BC的中点.(Ⅰ)求证:EF∥平面PAB;
(Ⅱ)求直线BE与平面PAB所成角的正弦值.
分析:(Ⅰ)取AD中点M,连接EM,MF,EF,证明平面EMF∥平面PAB,可得EF∥平面PAB;
(Ⅱ)证明PD⊥平面ABCD,求出BE,利用等体积求出E到平面PAB的距离,从而可求直线BE与平面PAB所成角的正弦值.
(Ⅱ)证明PD⊥平面ABCD,求出BE,利用等体积求出E到平面PAB的距离,从而可求直线BE与平面PAB所成角的正弦值.
解答: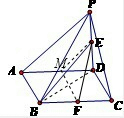 (Ⅰ)证明:取AD中点M,连接EM,MF,EF,则
(Ⅰ)证明:取AD中点M,连接EM,MF,EF,则
∵E,F分别是PD,BC的中点,
∴EM∥PA,MF∥AB
∵EM∩MF=M,PA∩AB=A
∴平面EMF∥平面PAB
∵EF?平面EMF
∴EF∥平面PAB;
(Ⅱ)解:∵二面角P-CD-A为直二面角,AD⊥DC
∴AD⊥平面PDC
∵PD?平面PDC,∴PD⊥AD
∵PD⊥DC,AD∩DC=D
∴PD⊥平面ABCD
设E到平面PAB的距离为h,连接BD,则BD=3
,
∵PD=4,∴PB=
,BE=
∵PA=5,AB=3,∴PA⊥AB,∴S△PAB=
×3×5=
∵S△PAE=
×2×3=3
∴由等体积可得:
×3×3=
×
×h,∴h=
∴直线BE与平面PAB所成角的正弦值为
=
.
 (Ⅰ)证明:取AD中点M,连接EM,MF,EF,则
(Ⅰ)证明:取AD中点M,连接EM,MF,EF,则∵E,F分别是PD,BC的中点,
∴EM∥PA,MF∥AB
∵EM∩MF=M,PA∩AB=A
∴平面EMF∥平面PAB
∵EF?平面EMF
∴EF∥平面PAB;
(Ⅱ)解:∵二面角P-CD-A为直二面角,AD⊥DC
∴AD⊥平面PDC
∵PD?平面PDC,∴PD⊥AD
∵PD⊥DC,AD∩DC=D
∴PD⊥平面ABCD
设E到平面PAB的距离为h,连接BD,则BD=3
| 2 |
∵PD=4,∴PB=
| 34 |
| 22 |
∵PA=5,AB=3,∴PA⊥AB,∴S△PAB=
| 1 |
| 2 |
| 15 |
| 2 |
∵S△PAE=
| 1 |
| 2 |
∴由等体积可得:
| 1 |
| 3 |
| 1 |
| 3 |
| 15 |
| 2 |
| 6 |
| 5 |
∴直线BE与平面PAB所成角的正弦值为
| ||
|
3
| ||
| 55 |
点评:本题主要考查了直线与平面平行的判定,以及线面角的度量,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
 如图所示,在直角梯形ABCD中,|AD|=3,|AB|=4,|BC|=
如图所示,在直角梯形ABCD中,|AD|=3,|AB|=4,|BC|=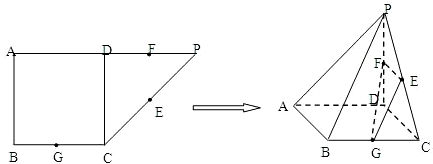
 如图所示,在直角梯形OABC中,
如图所示,在直角梯形OABC中,