题目内容
 如图所示,在直角梯形OABC中,∠COA=∠OAB=
如图所示,在直角梯形OABC中,∠COA=∠OAB=| π | 2 |
(1)求异面直线MN与BC所成的角;
(2)求MN与面SAB所成的角.
分析:(1)建立空间直角坐标系,求得相关点的坐标,再求相关向量的坐标,最后用向量夹角公式求解.
(2)欲求MN与面SAB所成的角的正弦值,先利用待定系数法求出平面SAB的一个法向量,最后用向量夹角公式求解即可
(2)欲求MN与面SAB所成的角的正弦值,先利用待定系数法求出平面SAB的一个法向量,最后用向量夹角公式求解即可
解答:解:(1)以OC,OA,OS所在直线建立空间直角坐标系O-xyz,则S(0,0,1),C(2,0,0),A(0,1,0),B(1,1,0)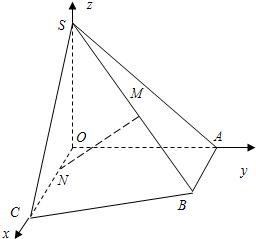 ,所以N(
,所以N(
,0,0),M(
,
,
)
∴
=(0,-
,-
),
=(1,-1,0)
∴直线MN与BC所成角的余弦值为
=
∴直线MN与BC所成角为
;
(2)设平面SAB的一个法向量为
=(a,b,c)
•
=(a,b,c)•(1,1,-1)=a+b-c=0
•
=(a,b,c)•(0,1,-1)=b-c=0
令b=1可得法向量
=(0,1,1)
∵
=(0,-
,-
),
∴直线MN与面SAB所成角的正弦值为|
|=
∴直线MN与面SAB所成角为
 ,所以N(
,所以N(| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| MN |
| 1 |
| 2 |
| 1 |
| 2 |
| BC |
∴直线MN与BC所成角的余弦值为
| ||||
|
|
| 1 |
| 2 |
∴直线MN与BC所成角为
| π |
| 3 |
(2)设平面SAB的一个法向量为
| n |
| n |
| SB |
| n |
| SA |
令b=1可得法向量
| n |
∵
| MN |
| 1 |
| 2 |
| 1 |
| 2 |
∴直线MN与面SAB所成角的正弦值为|
| ||||
|
|
| 1 |
| 2 |
∴直线MN与面SAB所成角为
| π |
| 6 |
点评:本题考查用向量法研究直线与平面所成的角和异面直线所成的角,选用向量法,避开了作辅助线,优越性很强,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
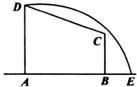 如图所示,在直角梯形ABCD中,|AD|=3,|AB|=4,|BC|=
如图所示,在直角梯形ABCD中,|AD|=3,|AB|=4,|BC|=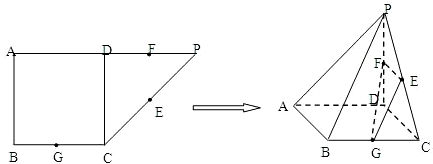
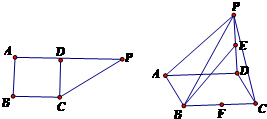 如图所示,在直角梯形ABCP中,AP∥BC,AB⊥AP,AB=BC=3,AP=7,CD⊥AP,现将△PCD沿折线CD折成直二面角P-CD-A,设E,F分别是PD,BC的中点.
如图所示,在直角梯形ABCP中,AP∥BC,AB⊥AP,AB=BC=3,AP=7,CD⊥AP,现将△PCD沿折线CD折成直二面角P-CD-A,设E,F分别是PD,BC的中点.