题目内容
如图,已知椭圆![]() 的离心率为
的离心率为![]() ,以该椭圆上的点和椭圆的左、右焦点F1,F2为顶点的三角形的周长为4(
,以该椭圆上的点和椭圆的左、右焦点F1,F2为顶点的三角形的周长为4(![]() +1).一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D.
+1).一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D.
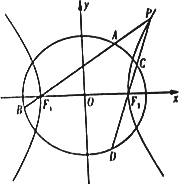
(Ⅰ)求椭圆和双曲线的标准方程;
(Ⅱ)设直线PF1、PF2的斜率分别为k1、k2,证明k1·k2=1;
(Ⅲ)是否存在常数λ,使得|AB|+|CD|=λ|AB|·|CD|恒成立?若存在,求λ的值;若不存在,请说明理由.
答案:

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

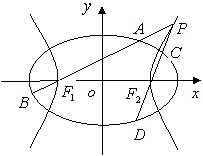 (Ⅰ)求椭圆和双曲线的标准方程;
(Ⅰ)求椭圆和双曲线的标准方程;  的离心率为
的离心率为 ,以该椭圆上的点和椭圆的左、右焦点
,以该椭圆上的点和椭圆的左、右焦点 为顶点的三角形的周长为
为顶点的三角形的周长为 .一等轴双曲线的顶点是该椭圆的焦点,设
.一等轴双曲线的顶点是该椭圆的焦点,设 为该双曲线上异于顶点的任一点,直线
为该双曲线上异于顶点的任一点,直线 和
和 与椭圆的交点分别为
与椭圆的交点分别为 和
和 .
.
 、
、 ,证明
,证明 ;
; ,使得
,使得 恒成立?若存在,求
恒成立?若存在,求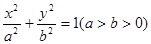 的离心率为
的离心率为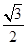 ,且经过点
,且经过点 平行于
平行于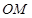 的直线
的直线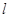 在
在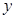 轴上的截距为
轴上的截距为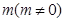 ,
, 的取值范围;
的取值范围;
 、
、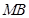 与
与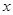 轴始终围成一个等腰三角形.
轴始终围成一个等腰三角形.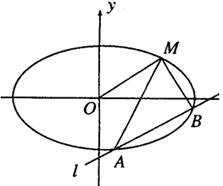
 的离心率为
的离心率为 ,以该椭圆上的点和椭圆的左右焦点F1、F2为顶点的三角形的周长为
,以该椭圆上的点和椭圆的左右焦点F1、F2为顶点的三角形的周长为 。一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的焦点分别为A、B和C、D。
。一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的焦点分别为A、B和C、D。 ,使得|AB|+|CD|=
,使得|AB|+|CD|=