题目内容
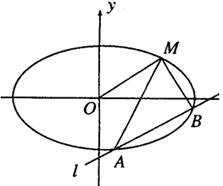
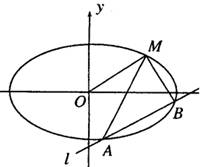
如图,已知椭圆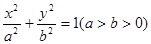 的离心率为
的离心率为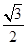 ,且经过点
,且经过点 平行于
平行于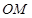 的直线
的直线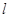 在
在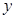 轴上的截距为
轴上的截距为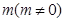 ,
,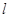 与椭圆有A、B两个
与椭圆有A、B两个
不同的交点
(Ⅰ) 求椭圆的方程;
(Ⅱ) 求 的取值范围;
的取值范围;
(III)求证:直线 、
、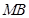 与
与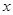 轴始终围成一个等腰三角形.
轴始终围成一个等腰三角形.
【答案】
【解析】本小题主要考查椭圆的标准方程,直线与椭圆的位置关系,考查转化与化归的思想方法,以及学生的运算能力.
解:(Ⅰ)设椭圆方程为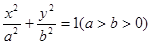 ………1分
………1分
离心率为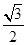 所以
所以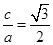 ,
,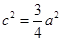 可得
可得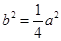
由经过点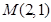 ,
,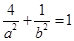
解得 ,
,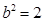 …………………………3分
…………………………3分
∴椭圆方程为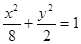 ……………………………4分
……………………………4分
(Ⅱ)∵直线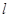 平行于
平行于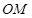 ,且在
,且在 轴上的截距为
轴上的截距为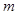
又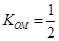
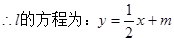 ……………………………………………………5分
……………………………………………………5分
由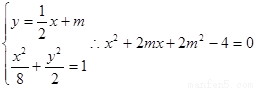 ……………………………………6分
……………………………………6分
∵直线l与椭圆交于A、B两个不同点,
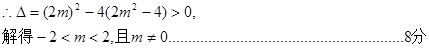
(III)设直线MA、MB的斜率分别为k1,k2,只需证明k1+k2=0即可…………9分
设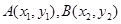 则
则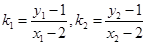
由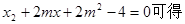
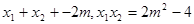 ……………………………………………………10分
……………………………………………………10分
而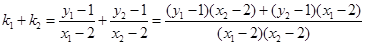
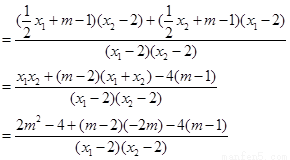
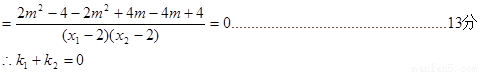
故直线MA、MB与x轴始终围成一个等腰三角形.……………………14分

练习册系列答案
相关题目

 (Ⅰ)求椭圆和双曲线的标准方程;
(Ⅰ)求椭圆和双曲线的标准方程;  的离心率为
的离心率为 ,以该椭圆上的点和椭圆的左、右焦点
,以该椭圆上的点和椭圆的左、右焦点 为顶点的三角形的周长为
为顶点的三角形的周长为 .一等轴双曲线的顶点是该椭圆的焦点,设
.一等轴双曲线的顶点是该椭圆的焦点,设 为该双曲线上异于顶点的任一点,直线
为该双曲线上异于顶点的任一点,直线 和
和 与椭圆的交点分别为
与椭圆的交点分别为 和
和 .
.
 、
、 ,证明
,证明 ;
; ,使得
,使得 恒成立?若存在,求
恒成立?若存在,求 的离心率为
的离心率为 ,以该椭圆上的点和椭圆的左右焦点F1、F2为顶点的三角形的周长为
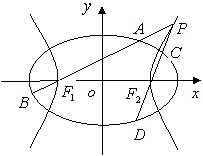
,以该椭圆上的点和椭圆的左右焦点F1、F2为顶点的三角形的周长为 。一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的焦点分别为A、B和C、D。
。一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的焦点分别为A、B和C、D。 ,使得|AB|+|CD|=
,使得|AB|+|CD|=