题目内容
“坐标法”是以坐标系为桥梁,把几何问题转化成代数问题,通过代数运算研究图形的几何性质的方法,它是解析几何中是基本的研究方法.请用坐标法证明:
已知圆C的方程是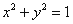 ,点
,点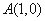 ,直线
,直线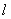 与圆C相交于P、Q两点(不同于A),
与圆C相交于P、Q两点(不同于A),
(Ⅰ)若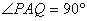 ,则直线
,则直线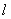 必经过圆心O;
必经过圆心O;
(Ⅱ)若直线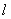 经过圆心O,则
经过圆心O,则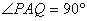 .
.
证明: (Ⅰ)设直线AP的方程是 ,
,
代入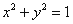 得
得 ---------------2分
---------------2分
因为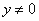 ,所以
,所以 ,从而得
,从而得 -------------4分
-------------4分
因为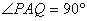 ,所以直线AQ的方程
,所以直线AQ的方程
以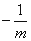 代换点Q坐标中的
代换点Q坐标中的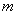 ,得
,得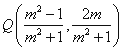 ----------------------5分
----------------------5分
当 时,直线OP、OQ的斜率分别为
时,直线OP、OQ的斜率分别为 ,显然
,显然
即直线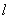 经过圆心O。--------------------------------------------6分
经过圆心O。--------------------------------------------6分
当 时,
时,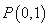 ,
, ,显然直线
,显然直线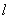 经过圆心O
经过圆心O
综上若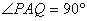 ,则直线
,则直线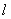 必经过圆心O。
必经过圆心O。


练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
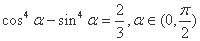 ,则
,则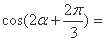 .
. 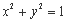 上任意一点P向y轴作垂线段PP`,交y轴于P`,则线段PP`的中点M的轨迹方程是 ;
上任意一点P向y轴作垂线段PP`,交y轴于P`,则线段PP`的中点M的轨迹方程是 ; 的直线
的直线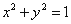 有公共点,则直线
有公共点,则直线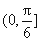 (B)
(B) (C)
(C) (D)
(D)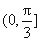
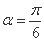 ,则
,则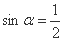 ”的否命题是假命题;
”的否命题是假命题;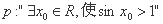 ,则
,则 ;
;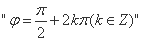 是“函数
是“函数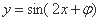 为偶函数”的充要条件;
为偶函数”的充要条件; ,命题
,命题 ,那么命题
,那么命题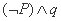 为真命题。
为真命题。 的棱长为1,若动点
的棱长为1,若动点 在线段
在线段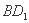 上运动,则
上运动,则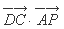 的取值范围_______________;
的取值范围_______________; 中,
中, ,且
,且 两两垂直,则该三棱锥外接球的表面积为
两两垂直,则该三棱锥外接球的表面积为 (B)
(B)
 (D)
(D)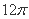
 在
在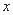 轴上且焦距为
轴上且焦距为 ,
, 为左右顶点,左准线
为左右顶点,左准线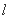 与
与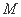 ,
,  ,若点
,若点 在直线
在直线 ,
, 的最大值为 .
的最大值为 .