题目内容
在数列{an}中，a1=2，an+1=2an-n+1，n∈N*
（1）证明：数列{an-n}是等比数列；
（2）求数列{an}的前n项和Sn．
（1）证明：∵an+1=2an-n+1
∴an+1-（n+1）=2（an-n），又a1-1=2≠0
∴数列{an-n}是首项为1，公比为2的等比数列（5分）
（2）解：由（1）可得
即
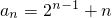（9分）
∴
=（1+2+…+2n-1）+（1+2+…+n）
=
（13）
分析：（1）由an+1=2an-n+1可得an+1-（n+1）=2（an-n），且a1-1=2≠0，可证
（2）由（1）可求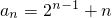，利用分组求和，结合等差数列与等比数列 的求和公式可求
点评：本题主要考查了利用构造法证明等比数列（主要是配凑定义符合的要求），分组求和方法及等差数列、等比数列的求和公式的应用．
∴an+1-（n+1）=2（an-n），又a1-1=2≠0
∴数列{an-n}是首项为1，公比为2的等比数列（5分）
（2）解：由（1）可得
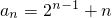即（9分）∴
=（1+2+…+2n-1）+（1+2+…+n）
=
（13）分析：（1）由an+1=2an-n+1可得an+1-（n+1）=2（an-n），且a1-1=2≠0，可证
（2）由（1）可求
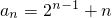，利用分组求和，结合等差数列与等比数列 的求和公式可求点评：本题主要考查了利用构造法证明等比数列（主要是配凑定义符合的要求），分组求和方法及等差数列、等比数列的求和公式的应用．
练习册系列答案
相关题目
，并且对任意n∈N*，n≥2都有an•an-1=an-1-an成立，令bn=
（n∈N*）．
}的前n项和为Tn，证明：
．