题目内容
对于曲线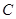 :
: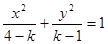 ,给出下面四个命题:
,给出下面四个命题:
①曲线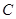 不可能表示椭圆; ②当
不可能表示椭圆; ②当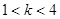 时,曲线
时,曲线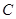 表示椭圆;
表示椭圆;
③若曲线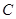 表示双曲线,则
表示双曲线,则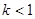 或
或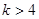 ;
;
④若曲线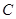 表示焦点在
表示焦点在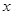 轴上的椭圆,则
轴上的椭圆,则 .
.
其中所有正确命题的序号为__ _ __ .
③④
解析试题分析:据椭圆方程的特点列出不等式求出k的范围判断出①②错,据双曲线方程的特点列出不等式求出k的范围,判断出③对;据椭圆方程的特点列出不等式求出t的范围,判断出④错。解:若C为椭圆应该满足(4-k)(k-1)>0,4-k≠k-1
即1<k<4 且k≠ 故①②错,若C为双曲线应该满足(4-k)(k-1)<0即k>4或k<1 故③对,若C表示椭圆,且长轴在x轴上应该满足4-k>k-1>0则 1<k<
故①②错,若C为双曲线应该满足(4-k)(k-1)<0即k>4或k<1 故③对,若C表示椭圆,且长轴在x轴上应该满足4-k>k-1>0则 1<k< ,故④对
,故④对
故答案为:③④.
考点:椭圆的方程,双曲线的方程
点评:本试题考查了椭圆和双曲线的方程的运用,属于基础题。

练习册系列答案
相关题目
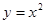 在
在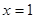 处的切线与两坐标轴围成三角形区域为
处的切线与两坐标轴围成三角形区域为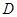 (包含三角形内部与边界).若点
(包含三角形内部与边界).若点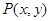 是区域
是区域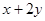 的取值范围是 .
的取值范围是 .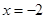 ,则抛物线的标准方程是______________。
,则抛物线的标准方程是______________。 中,抛物线
中,抛物线 上纵坐标为1的一点到焦点的距离为3,则焦点到准线的距离为_____________
上纵坐标为1的一点到焦点的距离为3,则焦点到准线的距离为_____________ ,曲线
,曲线 :
: 上的点到直线的距离为
上的点到直线的距离为 ,则
,则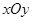 中,点
中,点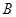 与点
与点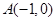 关于原点
关于原点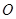 对称.点
对称.点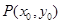 在抛物线
在抛物线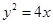 上,且直线
上,且直线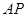 与
与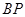 的斜率之积等于-
的斜率之积等于-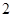 ,则
,则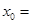 _____________
_____________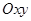 中,若双曲线
中,若双曲线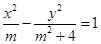 的焦距为8,则
的焦距为8,则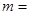
 的左右焦点分别为
的左右焦点分别为 ,焦距为
,焦距为 ,若直线
,若直线 与椭圆的一个交点满足
与椭圆的一个交点满足 ,则该椭圆的离心率等于_____
,则该椭圆的离心率等于_____