题目内容
1.在等比数列{an}中,公比q=-2,且a3a7=4a4,则a8与a11的等差中项为-56.分析 运用等比数列的性质,可得a3a7=a4a6,求得a6=4,运用等比数列的通项公式可得a8与a11的等差中项.
解答 解:∵在等比数列{an}中,公比q=-2,且a3a7=4a4,
a3a7=a4a6,
∴a6=4,∴${a_8}={a_6}{q^2}=16$,${a_{11}}={a_8}{q^3}=-128$,
则a8与a11的等差中项为$\frac{{{a_8}+{a_{11}}}}{2}=-56$.
故答案为:-56.
点评 本题考查等差数列的中项的性质和等比数列的通项公式的运用,考查方程思想,以及运算能力,属于中档题.

练习册系列答案
相关题目
6.命题?x∈R,tanx≠1,的否定是( )
| A. | ?x∉R,tanx≠1 | B. | ?x∈R,tanx=1 | C. | ?x0∉Rtanx0=1 | D. | ?x0∈R,tanx0=1 |
10.下列四个函数中,以π为最小正周期,且在区间$(\frac{π}{2},π)$上为增函数的是( )
| A. | y=sin2x | B. | y=|cosx| | C. | y=-tanx | D. | $y=cos\frac{x}{2}$ |
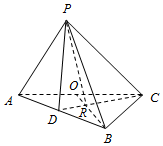 在三棱锥P-ABC中,AB⊥BC,AB=6,$BC=2\sqrt{3}$,O为AC的中点,过C作BO的垂线,交BO、AB分别于R、D.若∠DPR=∠CPR,则三棱锥P-ABC体积的最大值为3$\sqrt{3}$.
在三棱锥P-ABC中,AB⊥BC,AB=6,$BC=2\sqrt{3}$,O为AC的中点,过C作BO的垂线,交BO、AB分别于R、D.若∠DPR=∠CPR,则三棱锥P-ABC体积的最大值为3$\sqrt{3}$.