题目内容
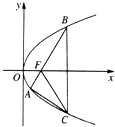
在直角坐标系中任给一条直线，它与抛物线y2=2x交于A、B两点，则
•
的取值范围为______．
| OA |
| OB |
设l：x=ty+b代入抛物线y2=2x，消去x得y2-2ty-2b=0．
设A（x1，y1），B（x2，y2），则y1+y2=2t，y1y2=-2b，
∴
•
=x1x2+y1y2=（ty1+b）（ty2+b）+y1y2=t2y1y2+tb（y1+y2）+b2+y1y2=b2-2b
=（b-1）2-1≥-1，
∴
•
的取值范围为[-1，+∞）．
故答案为：[-1，+∞）．
设A（x1，y1），B（x2，y2），则y1+y2=2t，y1y2=-2b，
∴
| OA |
| OB |
=（b-1）2-1≥-1，
∴
| OA |
| OB |
故答案为：[-1，+∞）．
练习册系列答案
相关题目
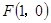的距离和到直线
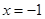的距离相等.若机器人接触不到过点
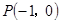且斜率为
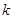的直线，则