题目内容
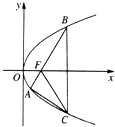
如图,已知△ABC的三个顶点都在抛物线y2=2px(p>0)上,抛物线的焦点F在AB上,AB的倾斜角为60°,|BF|=|CF|=4,则直线AC的斜率为______.

设A(x1,y1),B(x2,y2),则|AB|=x1+x2+p=
=
,
∴x1+x2=
,
∵x1x2=
,
∴x2=
,x1=
,
∴A(
,-
p),B(
,
p),
∵|BF|=|CF|=4,
∴C(
,-
p),
∴直线AC的斜率为
=-
.
故答案为:-
.
| 2p |
| sin260° |
| 8p |
| 3 |
∴x1+x2=
| 5p |
| 3 |
∵x1x2=
| p2 |
| 4 |
∴x2=
| 3p |
| 2 |
| p |
| 6 |
∴A(
| p |
| 6 |
| ||
| 3 |
| 3p |
| 2 |
| 3 |
∵|BF|=|CF|=4,
∴C(
| 3p |
| 2 |
| 3 |
∴直线AC的斜率为
-
| ||||||
|
| ||
| 2 |
故答案为:-
| ||
| 2 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
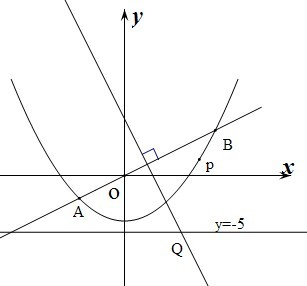
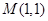 作斜率为
作斜率为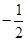 的直线与椭圆
的直线与椭圆 :
: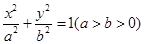 相交于
相交于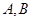 ,若
,若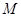 是线段
是线段 的中点,则椭圆
的中点,则椭圆