题目内容

（2012•包头一模）若圆C1：x2+y2+2ax+a2-4=0，（a∈R）与圆C2：x2+y2-2by-1+b2=0，（b∈R）外切，则a+b的最大值为（　　）
分析：利用两圆外切，圆心距等于半径之和，再利用基本不等式，即可求得a+b的最大值
解答：解：圆C1：x2+y2+2ax+a2-4=0的标准方程为（x+a）2+y2=4；圆C2：x2+y2-2bx-1+b2=0的标准方程为x2+（y-b）2=1
∵两圆外切，∴
a2+b2
=3
∵a2+b2≥2ab
∴2（a2+b2）≥（a+b）2
∴a+b≤3
2

∴a+b的最大值为3
2

故选D．
点评：本题考查两圆的位置关系，考查基本不等式的运用，正确运用基本不等式是关键．
练习册系列答案
相关题目
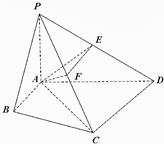（2012•包头一模）在四棱锥P-ABCD中，∠ABC=∠ACD=90°，∠BAC=∠CAD=60°，PA⊥平面ABCD，E为PD的中点，PA=2，AB=1．
（Ⅰ）求四棱锥P-ABCD的体积V；
（Ⅱ）若F为PC的中点，求证：平面PAC⊥平面AEF．
（2012•包头一模）下列命题错误的是（　　）
（2012•包头一模）已知双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）与抛物线y2=8x有 一个公共的焦点F，且两曲线的一个交点为P，若|PF|=5，则双曲线方程为
x2-
y2
3
=1
x2-
y2
3
=1
．
（2012•包头一模）函数f（x）=sin（ωx+?）（其中|?|＜
π
2
）的图象如图所示，为了得到y=sinωx的图象，只需把y=f（x）的图象上所有点（　　）
（2012•包头一模）在平面直角坐标系xoy中，曲线C1的参数方程为 
x=acosφ
y=bsinφ
（a＞b＞0，?为参数），在以O为极点，x轴的正半轴为极轴的极坐标系中，曲线C2是圆心在极轴上，且经过极点的圆．已知曲线C1上的点M（1，
3
2
）对应的参数φ=
π
3
，曲线C2过点D（1，
π
3
）．
（Ⅰ）求曲线C1，C2的直角坐标方程；
（Ⅱ）若点A（ρ 1，θ），B（ρ 2，θ+
π
2
） 在曲线C1上，求
1
ρ
2
1
+
1
ρ
2
2
的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网