Question

（09年扬州中学2月月考）（16分）已知为实数，数列满足，当时，，

（Ⅰ）；(5分)

（Ⅱ）证明：对于数列，一定存在，使；(5分)

（Ⅲ）令，当时，求证：(6分)

Answer 1

解析:（Ⅰ）由题意知数列的前34项成首项为100,公差为－3的等差数列,从第35项开始,奇数项均为3,偶数项均为1,从而=  ……(3分)

    =.  …………(5分)

   （Ⅱ）证明：①若,则题意成立…………………(6分)

②若,此时数列的前若干项满足,即.

设,则当时,.

从而此时命题成立…… (8分)

③若,由题意得,则由②的结论知此时命题也成立.

综上所述,原命题成立……………(10分)

（Ⅲ）当时，因为,

    所以=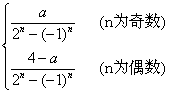……………(11分)

因为>0,所以只要证明当时不等式成立即可.

而

………(13分)

①当时,

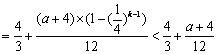
……(15分)

②当时,由于>0,所以<

综上所述,原不等式成立………(16分)