题目内容
过点(m,0)作圆x2+y2=1的切线交椭圆x2+4y2=4于A,B两点,则|AB|的最大值是( )
分析:设出直线AB所在的直线方程,由圆心到直线的距离等于圆的半径得到m和直线的斜率的关系式,再把直线方程和椭圆方程联立后化为关于x的一元二次方程,利用根与系数关系得到A,B两点的横坐标的和与积,代入弦长公式后转化为含有一个字母的函数关系,然后利用基本不等式求最值.
解答:解:设直线AB的方程为y=k(x-m),
由直线AB与圆x2+y2=1相切可知,圆心到直线的距离d=
=1,
化简得k2m2=k2+1.
将直线方程y=k(x-m)代入椭圆方程x2+4y2=4消y,得
(4k2+1)x2-8k2mx+4k2m2-4=0
设点A(x1,y1),B(x2,y2),
则x1+x2=
,x1x2=
|AB|=
|x1-x2|=
=
=
=
≤
=2
当且仅当|m|=
,即|m|=√3,m=±√3时,取等号
当直线AB与X轴垂直,切点为(±1,0),将x=±1代入椭圆方程求得y=±√3/2
∴此时|AB|=√3<2
综上,m=±√3,有|AB|最大值2.
由直线AB与圆x2+y2=1相切可知,圆心到直线的距离d=
| |km| | ||
|
化简得k2m2=k2+1.
将直线方程y=k(x-m)代入椭圆方程x2+4y2=4消y,得
(4k2+1)x2-8k2mx+4k2m2-4=0
设点A(x1,y1),B(x2,y2),
则x1+x2=
| 8k2m |
| 4k2+1 |
| 4k2m2-4 |
| 4k2+1 |
|AB|=
| 1+k2 |
| 1+k2 |
| (x1+x2)2-4x1x2 |
=
| 1+k2 |
(
|
=
4
| ||
| m2+3 |
4
| ||
| |m|+3|m| |
4
| ||
2
|
当且仅当|m|=
| 3 |
| |m| |
当直线AB与X轴垂直,切点为(±1,0),将x=±1代入椭圆方程求得y=±√3/2
∴此时|AB|=√3<2
综上,m=±√3,有|AB|最大值2.
点评:本题考查了直线与圆锥曲线的关系,考查了分类讨论得数学思想方法,训练了弦长公式的应用,考查了利用基本不等式求最值,考查了学生的运算能力,是有一定难度题目.

练习册系列答案
相关题目
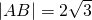 ,动点C的运动轨迹为曲线G,且当动点C运动时,cosC有最小值
,动点C的运动轨迹为曲线G,且当动点C运动时,cosC有最小值 .
.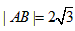 ,动点C的运动轨迹为曲线G,且当动点C运动时,cosC有最小值
,动点C的运动轨迹为曲线G,且当动点C运动时,cosC有最小值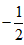 。
。