题目内容
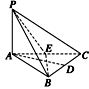如图所示，在三棱锥P—ABC中，PA⊥底面ABC，
（1）证明：平面PBE⊥平面PAC；
（2）如何在BC上找一点F，使AD∥平面PEF？并说明理由.
（1）证明略（2）取CD的中点F，则点F即为所求
解析:
（1）因为PA⊥底面ABC，所以PA⊥BE.
又因为△ABC是正三角形，且E为AC的中点，
所以BE⊥CA.
又PA∩CA=A，所以BE⊥平面PAC.
因为BE
平面PBE，所以平面PBE⊥平面PAC.
（2） 取CD的中点F，则点F即为所求.
因为E、F分别为CA、CD的中点，所以EF∥AD.
又EF平面PEF，AD
平面PEF，
所以AD∥平面PEF.
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
（2012•广州一模）如图所示，在三棱锥P-ABC中，
如图所示，在三棱锥P-ABC中，PA⊥面ABC，∠ABC=90°．该三棱锥中有哪些直角三角形，哪些面面垂直（只写结果，不要求证明）．
如图所示，在三棱锥P-ABC中，PA⊥面ABC，∠ABC=90°．
如图所示，在三棱锥P-ABC中，
如图所示，在三棱锥P-ABC中，PA⊥平面ABC，PA=1，AB⊥AC，AB=AC=2，E为AC的中点．